
- •1. Основные понятия математической статистики. Статистический эксперимент. Способы накопления статистической информации. Понятие выборки.
- •2. Примеры параметрических семейств распределений.
- •3.Виды задач математической статистики. Задачи точечного оценивания, доверительного оценивания, проверки статистических гипотез.
- •5.Постановка задачи точечного оценивания параметра. Риск оценки (квадратичный). Понятие состоятельности, несмещенности, асимптотической нормальности оценки.
- •6. Несмещенные оценки с равномерно-минимальной дисперсией. Минимаксный и байесовский подходы. Метод построения Байесовсих оценок.
- •7.Методы построения статистических оценок. Метод максимального правдоподобия и метод моментов. Примеры.
- •8. Регулярный эксперимент. Информация Фишера. Неравенство Рао-Крамера. Эффективные по Фишеру оценки.
- •9. Выборка из нормального распределения. Представление Хи-квадрат распределения с помощью нормальных. Распределение Стьюдента. Распределение Фишера-Снедекора. Лемма Фишера.
7.Методы построения статистических оценок. Метод максимального правдоподобия и метод моментов. Примеры.
Метод моментов построения статистических оценок. Примеры:
Пусть Х1,…,Хn
–выборка из распеределения с начальными
r
моментами i
порядка:
![]()
Они являются
функциями от неизвестных параметров
![]() .
.
Начальные выборочные
моменты i
порядка![]() .
.
Тогда метод моменов
состоит в приравнивании выборочных
![]() и теоретических
и теоретических
![]() моментов одного порядка:
моментов одного порядка:
![]() ,
где r
– выбирается сообразно тому, сколько
нбх уравнений для существования и
единственности решения, обычно
,
где r
– выбирается сообразно тому, сколько
нбх уравнений для существования и
единственности решения, обычно
![]()
Примеры.
1) распределение
Бернулли
![]()
![]()
![]() - теоретич. момент
- теоретич. момент
![]() - выборочный
момент
- выборочный
момент
Уравнение методом
моментов:
![]()
![]() - оценка методом
моментов (ММ)
- оценка методом
моментов (ММ)
2) распределение Лапласа DE(a,b)
![]()
![]()
![]() теор.
момент 1 порядка
теор.
момент 1 порядка
![]() теор момент 2
порядка
теор момент 2
порядка
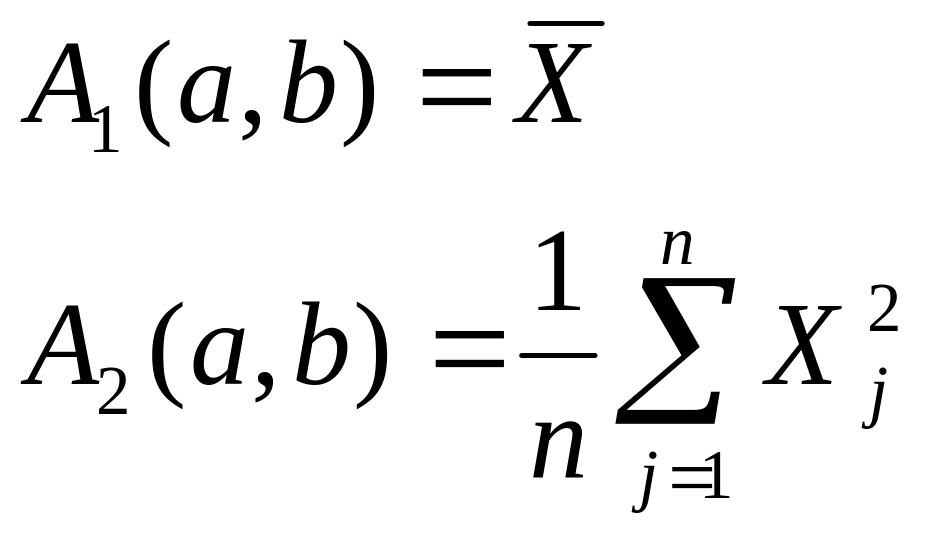 выбор. моменты
1 и 2 порядка
выбор. моменты
1 и 2 порядка
Уравнение ММ:
![]()
Оценки ММ:
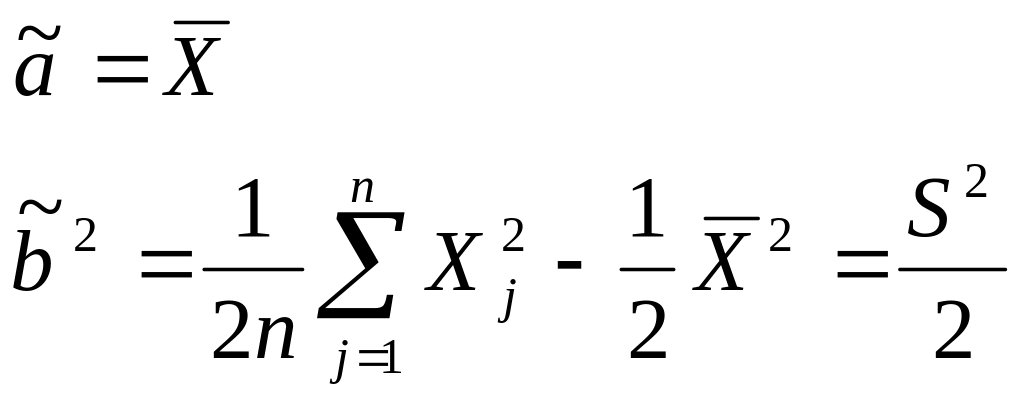
Метод максимального правдоподобия. Примеры:
Понятие правдоподобия
позволяет сравнивать вероятносные
шансы тех или иных исходов эксперимента
при различных значениях параметра
![]() .
.
В рез-те эксперимента поступает более точная информация, тогда прикаждом фикс. Значении естественно сравнивать достоверности исходов через значение плотности ( или производной Радона-Никодима) относительно некоторой домин. меры.
Пусть
![]() - семейство вероятностных мер, доминирующих
некоторой мерой
.
- семейство вероятностных мер, доминирующих
некоторой мерой
.
(если величины имеют абс. непрер. распределение, то мера Лебега,
если дискретное – можно выбрать считающую меру на мн-ве возможных значений результата эксперимента)
![]() - плотность
распределения.
- плотность
распределения.
Функция правдоподобия является плотностью распределения случайного вектора :
![]()
Опр-е
Оценка
![]() - называется оценкой
правдоподобия,
если для каждого
- называется оценкой
правдоподобия,
если для каждого
![]() из выборочного пространства
из выборочного пространства![]()
![]()
Пусть Х1,…,Хn
- выборка
из одномерного семейства
<<![]()
![]() - плотность
- плотность
Выбираем
![]() ,
т.е.
,
т.е.
![]()
и
![]()
![]() функция
правдоподобия
функция
правдоподобия
![]()
Идея метода макс.
правдоподобия состоит в отыскании
значения
![]() ,
максимизирующее правдоподобие, т.е.
,
максимизирующее правдоподобие, т.е.
В силу монотонности логарифма задача сводиться к максимизации логарифма правдоподобия.
И далее нахождения max:
![]()
Примеры.
1) распределение Бернулли
Х1,…,Хn ~ Bi(1,p)
![]() - считающая мера
на Z
- считающая мера
на Z
Функция правд-я
![]()
![]()
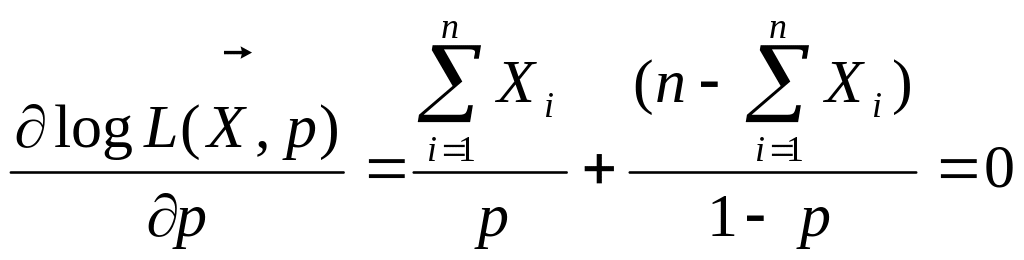
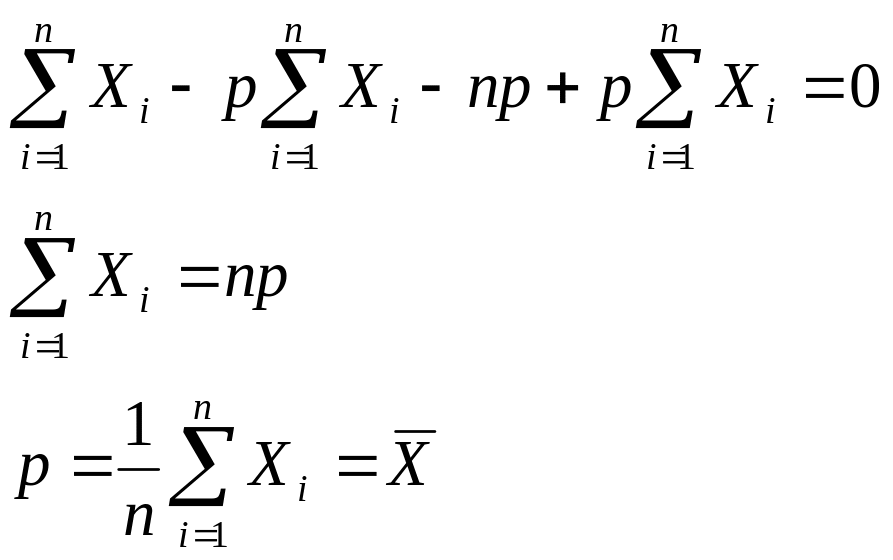
- оценка макс. правдоподобия
2)нормальное
распределение Х1,…,Хn
~ N(a,b),
![]()
![]()
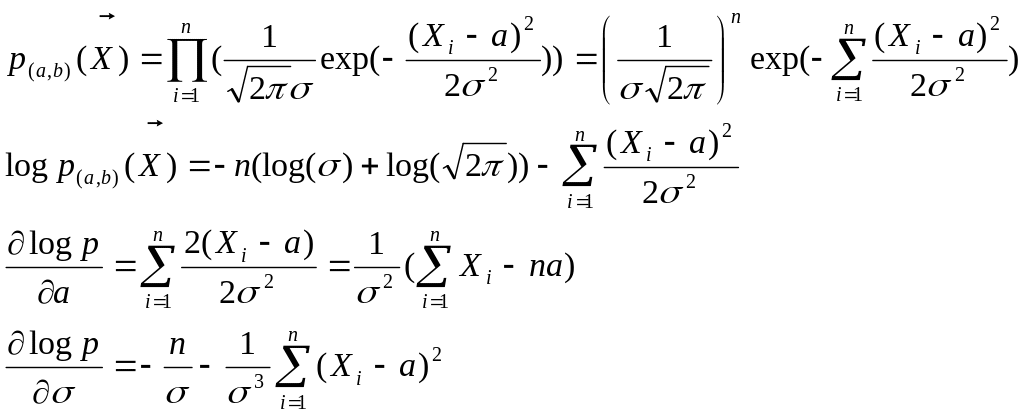
решаем уравнение
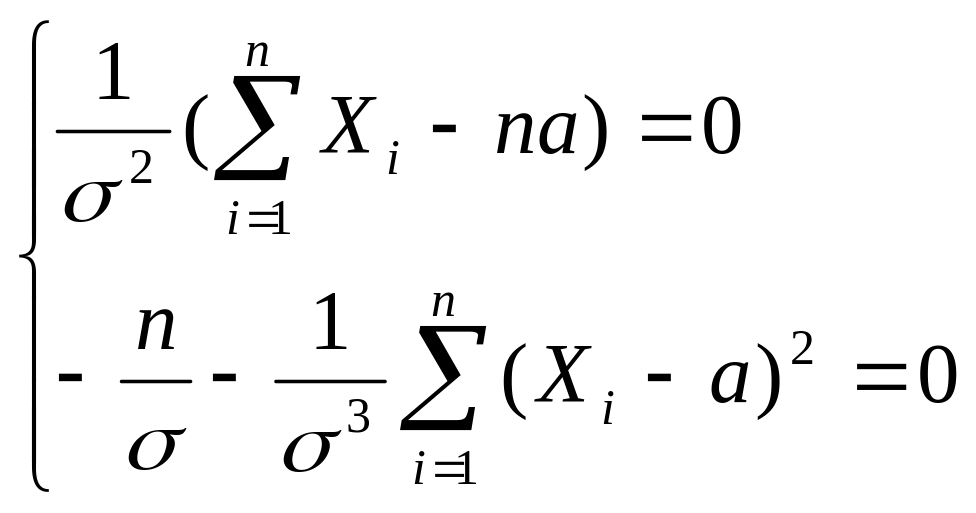
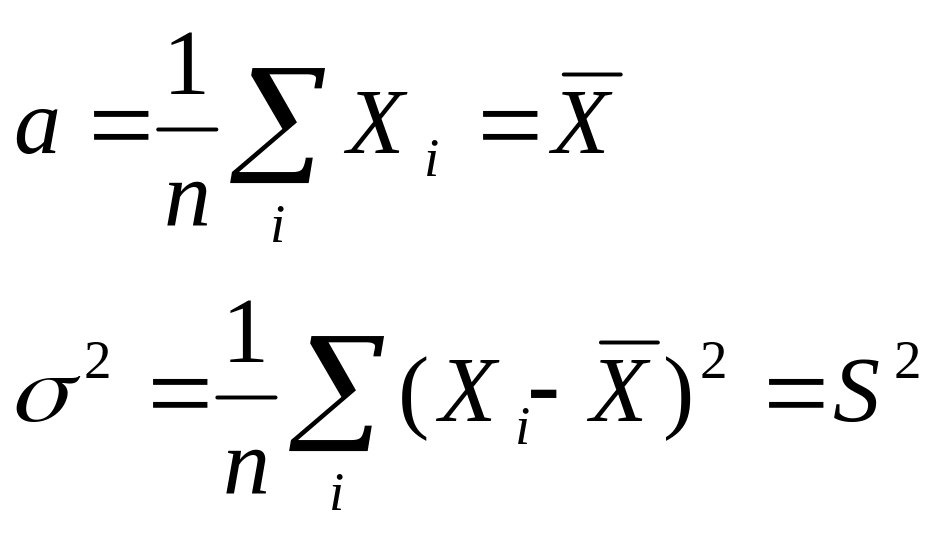
![]()
8. Регулярный эксперимент. Информация Фишера. Неравенство Рао-Крамера. Эффективные по Фишеру оценки.
Регулярный эксперимент:
Пусть x1..xn выборкаиз P(ро)={Pθ :θ€ΘcR}-сем-во однопарам, существ мера μ доминирующая сем-во P(ро) μ>>P(ро) с плотностями Pθ условие регулярности :
Эксперимент (сем-во) наз-ся реулярным если1) Pθ непрерывно дифф-мо по θ 2) В условиях сем-ва допускаются диффер-ное под знаком ∫ :
∂\∂θ∫Pθ(x~)μ(dx)=∫∂Pθ(x~)/∂θ*μ(dx)=0 3) Существ I(θ): I(θ)€(0..∞) ; I(θ)=∫[(Pθ’(x~))2/Pθ(x)]*μ(dx)=∫(Pθ’(x)/Pθ(x))2*Pθ(x)
[pθ’(x)=pθ(x)/∂θ] ; μ(dx)=Eθ[(lnpθ(x~))’]2 ;pθ(x~)=L(x¬,θ)-ф-ция правдоп. I(θ)-информ Фишера[характеризует наск-ко сильно различаются плотности возле (.)-ки пар-ра θ] С ростом кол-ва наблюдений инфор-ция накапливается
Неравенство Рао-Крамера. Эффективные по Фишеру оценки.
Пусть X1…Xn
– выборка
из P
={Pθ:
θ є Ĥ![]() R}
– семейство однопараметрическое,
R}
– семейство однопараметрическое,
![]() мера
доминирующая семейство P:
>> P
с плотностями Pθ.
Условие регулярности:
мера
доминирующая семейство P:
>> P
с плотностями Pθ.
Условие регулярности:
эксперимент (семейство) называется регулярным если:
Pθ непрерывно дифференцируема по
В условиях семейства допускается дифференцирование под знаком интеграла.
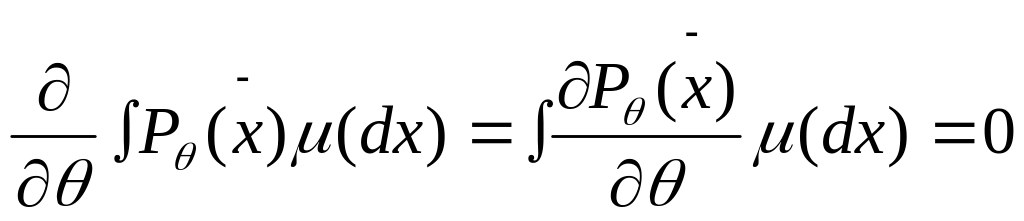
3. I( ) : I( ) (0, )
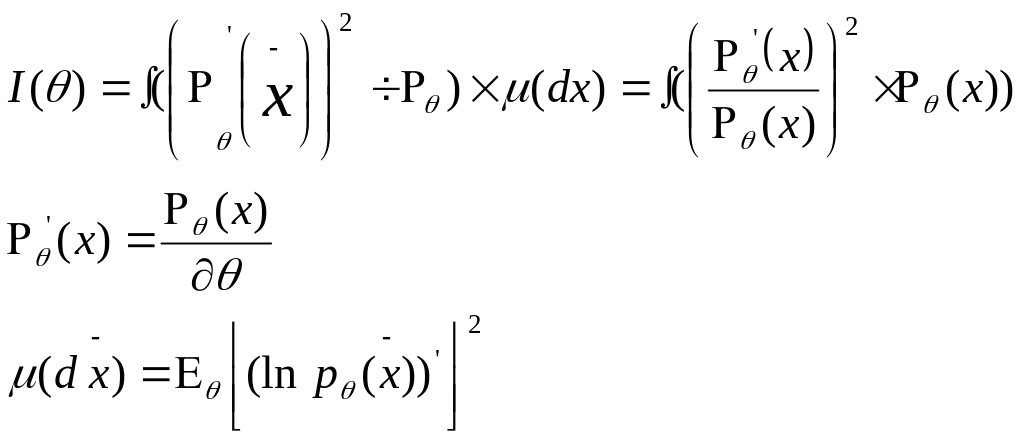
![]() -
функция правдоподобия
-
функция правдоподобия
![]() - информация Фишера
(характеризует, насколько сильно
различаются плотности возле точки
параметра
).
- информация Фишера
(характеризует, насколько сильно
различаются плотности возле точки
параметра
).
С ростом количества наблюдений информация накапливается.
Свойства информации.
Теорема: Пусть имеются 2 независимых экспиремента:
![]()
![]()
P1 ={P1θ, θ є Ĥ} P2 ={P2θ, θ є Ĥ}
Рассмотрим экспиремент:
![]()
![]() - т.е. 2 независимых
эксперимента
- т.е. 2 независимых
эксперимента
Пусть оба они
регулярны :
![]() и
и
Тогда эксперимент
общий
![]() тоже
регулярный, а
тоже
регулярный, а
![]()
Док-во:
Пусть исходные семейства были регулярны,
тогда по св1 регулярности ρ1
и ρ2 ,
следовательно
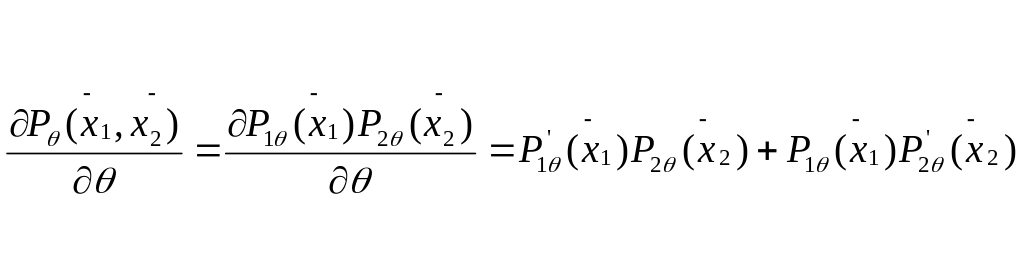
Следовательно свойство 1 выполнено для ρ.
Свойство 2: Рассмотрим
![]()
Свойство 3: {сложение
информации}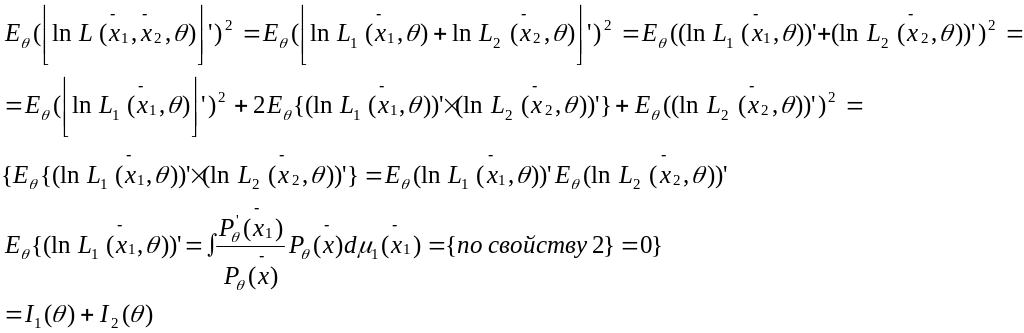 Замечание:
В условиях регулярного эксперимента
Замечание:
В условиях регулярного эксперимента
![]() (
log
L
(
log
L
![]() =0
=0
Неравенство Рао-Крамера (теорема).
Оценка δ –
разрешенная, если
![]() .
.
{диф-ние под знаком интеграла}
Пусть
![]() -
регулярный эксперимент, причем
- информация Фишера и
-
регулярный эксперимент, причем
- информация Фишера и
![]() -
разрешенная оценка, b(
)
=
-
разрешенная оценка, b(
)
=
![]() -
-смещение
оценки
.
Тогда
-
-смещение
оценки
.
Тогда
![]() и
и
![]()
![]() +
+![]()
-дает нижнюю границу для оценки (нер-во Крамера)
Следствие: Если
-
несмещенная, то
![]()
Док-во:
Отметим
![]() .
Поскольку
-
разрешенная
.
Поскольку
-
разрешенная
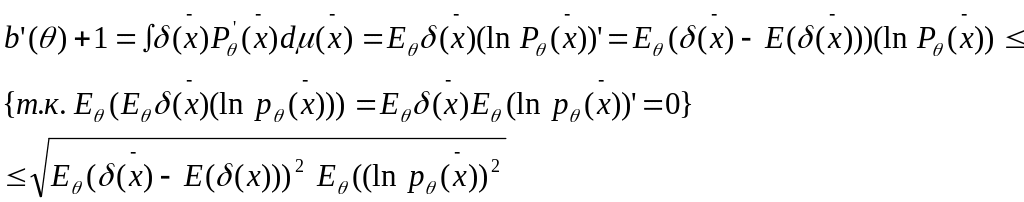
![]()
1-е нер-во.
Т.к.
![]()
![]()
Значение информации в знаменателе характеризует информацию в исх. данных для того, чтобы оценить параметр
Когда бывает равенство в нер-ве Рао-Крамера?
Рав-во достигается в том и только в том случае
(*)
![]()
1. Рав-во Коши-Бун-ко,
когда (*) пропорц-но x
![]() -
const
но зависит от парам-ра, принимает разные
значения
-
const
но зависит от парам-ра, принимает разные
значения
(**)
 -
однопараметрич. экспотенциальное
семейство
-
однопараметрич. экспотенциальное
семейство
Т.е. рав-во возможно в случае экспотенц. сем-ва
2. Из (**) берем
![]()
Пусть эксперимент
регулярен и
![]() ;
если это условие выполнено, тогда
;
если это условие выполнено, тогда![]() .
Покажем
.
Покажем
![]()
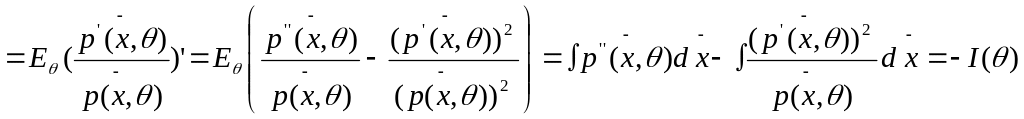
Оценка называется эффективной по Фишеру, если
a)
![]() - несмещенная {только в эксп.семействах}
- несмещенная {только в эксп.семействах}
b)
![]() -только для правельных пар-ров
-только для правельных пар-ров
