Уравнение бегущей волны

        Уравнение плоской одномерной синусоидальной волны:

        (Вместо синуса можно написать косинус.) Это уравнение отличается от уравнения синусоидальных колебаний тем, что колеблющая величина S зависит не только от времени, но и от координаты. Это и понятно: вместо одного маятника мы имеем множество связанных маятников - частиц среды. v - скорость распространения волны, А - амплитуда волны, аргумент синуса - фаза волны, _ - начальная фаза колебаний в точке х = 0,  - частота (циклическая) волны.

        Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется ДЛИНОЙ ВОЛНЫ  = .

        ВОЛНОВОЕ ЧИСЛО k:

        С помощью введенного волнового числа уравнение волны запишется:

        Если мы рассматриваем не одномерную волну, удобно наряду с волновым числом ввести ВОЛНОВОЙ ВЕКТОР k, модуль которого равен волновому числу, а направление совпадает с направлением луча (направлением распространения волны). В векторном виде уравнение волны будет выглядеть так:

здесь r - радиус вектор точки пространства; _- начальная фаза колебаний в начале координат.

     Уравнение сферической волны отличается тем, что амплитуда волны убывает с расстоянием от источника:

_= const по смыслу формулы есть амплитуда волны на единичном расстоянии от источника.

        Уравнение волны в дифференциальной форме обычно называют волновым уравнением; вид этого уравнения следующий:

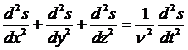     или     

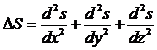
        Уравнение синусоидальной волны является решением волнового уравнения (можно проверить подстановкой). Общее же решение волнового уравнения следующее:

        Здесь А и В - произвольные константы, а f₁ и f₂ - произвольные дважды дифференцируемые функции. Первое слагаемое описывает волну, распространяющуюся слева направо, второе - встречную волну.

Волновое уравнение, дифференциальное уравнение с частными производными, описывающее процесс распространения возмущений в некоторой среде. В случае малых возмущений и однородной изотропной среды В. у. имеет вид:

  

где х, у, z — пространственные переменные, t — время, u = u (х, у, z) — искомая функция, характеризующая возмущение в точке (х, у, z) в момент t, а — скорость распространения возмущения. В. у. является одним из основных уравнений математической физики и широко используется в приложениях. Если u зависит только от двух (одной) пространственных переменных, то В. у. упрощается и называется двумерным (одномерным). В. у. допускает решение в виде "расходящейся сферической волны":

  u = f (t - r/a)/r,

где f — произвольная функция, a

  

  Особый интерес представляет так называемое элементарное решение (элементарная волна):

  u = δ (t - r/a)/r

(где δ — дельта-функция), дающее процесс распространения возмущения, произведённого мгновенным точечным источником (действовавшим в начале координат при t = 0). Образно говоря, элементарная волна представляет собой "бесконечный всплеск" на окружности r = at, удаляющийся от начала координат со скоростью а с постепенным уменьшением интенсивности. При помощи наложения элементарных волн можно описать процесс распространения произвольного возмущения.

  Малые колебания струны описываются одномерным В. у.:

  

Ж. Д'Аламбер предложил (1747) метод решения этого В. у. в виде наложения прямой и обратной волн: u = f (x - at) + g(x + at), а Л. Эйлер (1748) установил, что функции f и g определяются заданием так называемых начальных условий.

  Лит.: Тихонов А. Н. и Самарский А. А., Уравнения математической физики, 3 изд., М., 1966.

  П. И. Лизоркин.

Энергетические характеристики упругих волн

Распространение бегущих волн связано с передачей энергии от одной колеблющейся точки к другой.Перенос энергии бегущей волной объясняется тем,что максимум как кинетической .так и потенциальной энергии в такой волне приходится на точку волны,которая проходит положение равновесия.Передача энергии в бегущей волне происходит с той же скоростью,с которой распространяется фаза колебаний.Энергия ,переносимая волной, прямо пропорциональна плотности среды, квадрату амплитуды колебаний и квадрату их частоты.

Объёмная плотность кинетической энергии среды:ωk=dW/dV=ρυ²/2

Объёмная плотность потенциальной энергии упругодеформированной среды: ωp=dW/dV=ρυ²ε²/2

       Под объёмной плотностью энергии упругих волн понимают объёмную плотность ω механической энергии среды, обусловленную распространением этих волн и равную сумме ω кинетической и ω потенциальной.

Элементы специальной теории относительности.