Характеристики колебательного процесса.

1. Смещение х - отклонение колеблющейся точки от положе ния равновесия в данный момент времени (м).

2. Амплитуда х_м - наиболь шее смещение от положения рав новесия (м). Если колебания незатухающие, то амплитуда постоянна.

 

3. Период Т — время, за которое совершается одно полное колебание. Выражается в секундах (с).

За время, равное одному периоду (одно полное колебание) тело совершает перемещение, равное __       и проходит путь, равный ____ .

 

 

4. Частота   — число полных колеба ний за единицу времени. В СИ измеряется в герцах (Гц).

Частота колебаний равна одному герцу, если за 1 секунду совершается 1 полное колебание. 1 Гц= 1 с^-1.

 

 

5. Циклической (круговой) частотой  периодических колебаний наз. число полных колебаний, которые совершаются за 2 единиц времени (секунд). Единица измерения – с^-1.

 

 

6. Фаза колебания -  - физическая величина, определяющая смещение x в данный момент времени. Измеряется в радианах (рад).

Фаза колебания в начальный момент времени (t=0) называется начальной фазой (₀).

 

Гармонические колебания

Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями.

Например, в случае механических гармонических колебаний:.

В этих формулах ω – частота колебания, x_m – амплитуда колебания, φ₀ и φ₀’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ₀’ = φ₀ +/2 полностью совпадают.

 

 

 

Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0  смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ₀’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=х_m, следовательно, удобнее пользоваться функцией cos и φ₀=0.

 

Выражение, стоящее под знаком cos или sin, наз. фазой колебания:  .

 

Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.

 

Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).

Сложение гармонических колебаний одного направления и одинаковой частоты.

Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты

Воспользовавшись методом вращающегося вектора амплитуды Построим векторные диаграммы этих колебаний (рис.203). Так как векторы a1 и А2 вращаются с одинаковой угловой скоростью ₀, то разность фаз (₂-₁) между ними остается постоянной.

Очевидно, что уравнение результирующего колебания будет

х=х₁+х₂=Аcos(₀t+).

В выражении амплитуда А и начальная фаза соответственно задаются соотношениями

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (₂-₁) складываемых колебаний.

Проанализируем выражение в зависимости от разности фаз (₂-₁):

1) ₂-₁=±2m (m = 0, 1, 2,...), тогда A=A₁+A₂, т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;

2) ₂-₁= ±(2m+1) (m=0, 1, 2,...), тогда A = ¦A₁-A₂¦, т.е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.

Для практики особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.

Пусть амплитуды складываемых колебаний равны А, а частоты равны и +, причем <<. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

Складывая эти выражения и учитывая, что во втором сомножителе /2<<, найдем

Получившееся выражение есть произведение двух колебаний. Так как <<, то сомножитель, стоящий в скобках, почти не изменяется, когда сомножитель cost совершит несколько полных колебаний. Поэтому результирующее колебание х можно рассматривать как гармоническое

с частотой , амплитуда А_б, которого изменяется по следующему периодическому закону:

Частота изменения A_б, в два раза больше частоты изменения косинуса (так как берется по модулю), т.е. частота биений равна разности частот складываемых колебаний: _б=. Период биений

T_б=2/.

Характер зависимости (144.3) показан на рис. 204, где сплошные жирные линии дают график результирующего колебания, а огибающие их -- график медленно меняющейся по уравнению амплитуды.

Определение частоты тона (звука определенной высоты) биений между эталонным и измеряемым колебаниями -- наиболее широко применяемый на практике метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т.

Любые сложные периодические колебания s=f(t) можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, кратными циклической частоте _0:

Представление периодической функции в виде связывают с понятием гармонического анализа сложного периодического колебания, или разложенияФурье.

Члены ряда Фурье, определяющие гармонические колебания с частотами ₀, 2₀, 3₀,..., называются первой (или основной),

второй, третьей и т. д. гармониками сложного периодического колебания.

Резонанс

Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты со. Механические и электромагнитные колебания будем рассматривать одновременно, называя колеблющуюся величину либо смещением (х) колеблющегося тела из положения равновесия, либо зарядом (Q) конденсатора.

Из формулы следует, что амплитуда А смещения (заряда) имеет максимум. Чтобы определить резонансную частоту _рез -- частоту, при которой амплитуда А смещения (заряда) достигает максимума,-- нужно найти максимум функции или, что то же самое, минимум подкоренного выражения. Продифференцировав подкоренное выражение по и приравняв нулю, получим условие, определяющее _рез:

-4(²₀-²)+8²=0. Это равенство выполняется при =0, ±(²₀-2²), у которых только лишь положительное значение имеет физический смысл. Следовательно, резонансная частота

_рез=(²₀ -2²).

Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте _рез называется резонансом (соответственно механическим или электрическим). При ²<<² значение _рез практически совпадает с собственной частотой ₀ колебательной системы.

На рис. 210 приведена зависимость амплитуды вынужденных колебаний от частоты при различных значениях б. Из вытекает, что чем меньше б, тем выше и правее лежит максимум данной кривой. Если 0, то все кривые приходят к одному и тому же, отличному от нуля, предельному значению x₀/²₀, так называемомустатическому отклонению.

В случае механических колебаний x₀/²₀=F₀/(m²₀), в случае электромагнитных -- U_m/(L²₀). Если , то все кривые асимптотически стремятся к нулю. Приведенная совокупность кривых называется резонансными кривыми.

Из формулы вытекает, что при малом затухании (²<<²₀) резонансная амплитуда смещения (заряда)

где Q -- добротность колебательной системы, х₀/²₀ -- рассмотренное выше статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше A_рез. На рис. 211 представлены резонансные кривые для амплитуды скорости (тока). Амплитуда скорости (тока) максимальна при (_рез=₀ и равна x₀/(2), т. е. чем больше коэффициент затухания 8, тем ниже максимум резонансной кривой.

Используя формулы, получим, что амплитуда скорости при механическом резонансе равна (А_v)_max=х_а/(2)=F₀/r, а амплитуда тока при электрическом резонансе

(А_I)_max=x₀/(2)=U_m/R.

Из выражения tg=2/(²₀-²) следует, что если затухание в системе отсутствует (=0), то только в этом случае колебания и вынуждающая сила (приложенное переменное напряжение) имеют одинаковые фазы; во всех других случаях 0.

Зависимость от при разных коэффициентах б графически представлена на рис. 212, из которого следует, что при изменении изменяется и сдвиг фаз .

Из формулы вытекает, что при =0 =0, а при =₀ независимо от значения коэффициента затухания =/2, т. е. сила (напряжение) опережает по фазе колебания на р/2. При дальнейшем увеличении сдвиг фаз возрастает и при (>>0 , т.е. фаза колебаний почти противоположна фазе внешней силы (переменного напряжения). Семейство кривых, изображенных на рис. 212, называется фазовыми резонансными кривыми. Явления резонанса могут быть как вредными, так и полезными. Например, при конструировании машин и различного рода сооружений необходимо, чтобы собственная частота колебаний их не совпадала с частотой возможных внешних воздействий, в противном случае возникнут вибрации, которые могут вызвать серьезные разрушения. С другой стороны, наличие резонанса позволяет обнаружить даже очень слабые колебания, если их частота совпадает с частотой собственных колебаний прибора. Так, радиотехника, прикладная акустика, электротехника используют явление резонанса.

Дифференциальное уравнение свободных затухающих колебаний линейной системы задается в виде

                                                 (146.1)

где s – колеблющаяся величина, описывающая тот или иной физический процесс, =const — коэффициент затухания, ₀ — циклическая частота свободныхнезатухающих колебаний той же колебательной системы, т. е. при =0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.

Решение уравнения (146.1) рассмотрим в виде

                                                      (146.2)

где u=u(t). После нахождения первой и второй производных выражения (146.2) и подстановки их в (146.1) получим

                                                     (146.3)

Решение уравнения (146.3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай, когда этот коэффициент положителен:

                                                  (146.4)

(если ( )>0, то такое обозначение мы вправе сделать). Тогда получим уравнение типа (142.1) ü+²и=0, решением которого является функцияи=А₀cos(t+) (см. (140.1)). Таким образом, решение уравнения (146.1) в случае малых затуханий ( )

                                         (146.5)

где

                                                 (146.6)

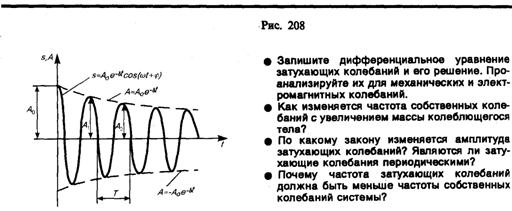
— амплитуда затухающих колебаний, а А₀ — начальная амплитуда. Зависимость (146.5) показана на рис. 208 сплошной линией, а зависимость (146.6) — штриховыми линиями. Промежуток времени =1/, в течение которого амплитуда затухающих колебаний уменьшается в е раз, называется временем релаксации.

Затухание нарушает периодичность колебаний, поэтому затухающие колебания не являются периодическими и, строго говоря, к ним неприменимо понятие периода или частоты. Однако если затухание мало, то можно условно пользоваться понятием периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины (рис. 208). Тогда период затуха ющих колебаний с учетом формулы (146.4) равен

Если A(t) и А(t + Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение

называется декрементом затухания, а его логарифм

                                                   (146.7)

— логарифмическим декрементом затухания; N_e — число колебаний, совершаемых за время уменьшения амплитуды в е раз. Логарифмический декремент затухания — по стоянная для данной колебательной системы величина.

Для характеристики колебательной системы пользуются понятием добротности Q, которая при малых значениях логарифмического декремента равна

                                                       (146.8)

(так как затухание мало ( ), то T принято равным Т₀).

Из формулы (146.8) следует, что добротность пропорциональна числу колебаний N_e, совершаемых системой за время релаксации.

Выводы, полученные для свободных затухающих колебаний линейных систем, применимы для колебаний различной физической природы — механических (в качестве примера рассмотрим пружинный маятник) и электромагнитных (в качестве примера рассмотрим электрический колебательный контур).

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:  .

Добротность

Материал из Википедии — свободной энциклопедии

Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.

Общая формула для добротности любой колебательной системы:

,

где:

• f₀ — резонансная частота колебаний

• W — энергия, запасённая в колебательной системе

• P_d — рассеиваемая мощность.

Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах - на зеркалах.

Для последовательного Колебательного контура в RLC цепях, в котором все три элемента включены последовательно:

,

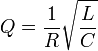где R, L и C — сопротивление, индуктивность и ёмкость резонансной цепи, соответственно.

Для параллельного контура, в котором индуктивность, емкость и сопротивление включены параллельно:

,

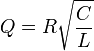ЛАФЧХ колебательных звеньев с разной добротностью.

Для электрической цепи гораздо проще измерить амплитуду (ток или напряжение), чем энергию или мощность. Поскольку мощность и энергия пропорциональны квадрату амплитуды осцилляции, полоса на АЧХ будет   от пика (примерно −3 дБ, а 1/2 это −6 дБ). Поэтому чаще используется другое эквивалентное определение добротности, которое связывает ширину амплитудной резонансной кривой Δω по уровню   с круговой частотой резонанса ω₀ = 2πf₀:

,

где: δ - коэффициент затухания, равный полуширине резонансной кривой, N_e — число колебаний за время релаксации.