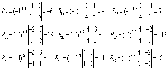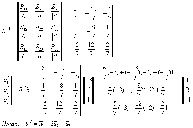- •1.Матрицы. Основные понятия. Виды матриц.
- •2.Линейные операции над матрицами. Св-ва операций.
- •3.Нелинейные операции над матрицами. Св-ва операций.
- •4. Определители. Основные понятия. Свойства определителей.
- •Свойства определителей
- •5.Вычисление определителей 2-го и 3-го порядков. Св-ва определит.(сумма опред., тождественные преобраз., сумма произвед. Эл-ов строк и столбцов)
- •Свойства определителей
- •6.Определители. Минор. Алгебраическое дополнение. Теорема Лапласа.
- •1. Метод окаймляющих миноров
- •2. Метод элементарных преобразований
- •Билет 11. Понятие линейной зависимость и линейной независимости строк (столбцов) матрицы. Теорема о ранге матрицы.
- •12. Системы линейных алгебраических уравнений (слау). Основные понятия. Матричная форма записи слау.
- •13. Системы лин.Ур-ий. Реш-ие сист. Лин. Ур-ий. Теорема Кронекера-Капелли.
- •14. Решение невырожденных систем линейных ур-ий. Теорема Крамера. Привести пример решения слау методом Крамера.
- •1 6. Решение систем линейных ур-ий методом исключения Гаусса (алгоритм решения, достоинства и недостатки данного метода).
- •Пример расчета межотраслевого баланса
- •22. Векторное произведение. Представление в виде определителя. Ориентация результирующего вектора. Модуль векторного произведения, его геометрический смысл.
- •23.Общее определение линейного пространства. Линейное векторное пространство. Примеры линейных пространств.
- •25. Определение скалярного произведения векторов в n-мерном векторном пространстве, его свойства. Евклидово действительное пространство. Ортогональный и ортонормированный базис в пространстве.
- •26. Собственные векторы матриц. Собственные числа матриц. Характеристическое уравнение. Базис определяемый собственными векторами матрицы.
- •27. Виды систем координат на плоскости. Уравнения связи декартовых и полярных координат. Примеры.
- •28. Прямая на плоскости. Виды задания прямой на плоскости. Взаимное расположение прямых на плоскости.
- •32.Плоскость в трехмерном пространстве. Виды задания пл-тей.
22. Векторное произведение. Представление в виде определителя. Ориентация результирующего вектора. Модуль векторного произведения, его геометрический смысл.
Векторное произведение векторов: ( с = [ab] = [a,b])
1)
векторсназывается
векторным произведением, не
компланарных(лежат не в одной плоскости)
векторов a
и b,
если его длина равна произведению длин
векторов aиb
на синус угла между ними :
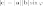 ;
;
2) векторcортогонален(перпендикулярен) векторам a и b;
3) векторы a, bиcобразуют правую тройку.
Свойства векторного произведения: (алгебраические)
1 )д
ля
любых векторов a,
bиc,
и действительного числа Л выполняется
следующее свойство: [ a
, b]
= - [ b
, a]
;
)д
ля
любых векторов a,
bиc,
и действительного числа Л выполняется
следующее свойство: [ a
, b]
= - [ b
, a]
;
2 ) [ a + b , c] = [ a + c ] + [ b , c ] ;
3) [λa , b ] = Л [ a , b ].
Геометрически свойства векторного произведения:
1)модуль вектороного произведения чесленно равен площади параллелограмма, построенного на векторах aи b;
2) векторное произведение = нулевому вектору, тогда и только тогда, когда множители коллинеарны(если они лежат на параллельных прямых или на одной прямой).
Представление в виде определителя:
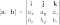
Если
система координат левая, то их векторное
произведение имеет вид:
Результирующий вектор- средний вектор, т. е. векторная сумма составляющих векторов. Вычисляется за некоторый период времени.
23.Общее определение линейного пространства. Линейное векторное пространство. Примеры линейных пространств.
Л инейным
(векторным) пространством называется
множество Vпроизвольных
элементов, названных векторами, в
котором определены операции сложения
и умножения вектора на число.
инейным
(векторным) пространством называется
множество Vпроизвольных
элементов, названных векторами, в
котором определены операции сложения
и умножения вектора на число.
С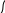 умма
:U
+ V,
U,
V
умма
:U
+ V,
U,
V Vлинейные
операции
Vлинейные
операции
Умножение: λ*U, U V
Аксиомы (свойства) линейного пространства:
1)
 ,
для любых
,
для любых 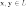 (коммутативность
сложения);
(коммутативность
сложения);
2)
 ,
для любых
,
для любых  (ассоциативность
сложения);
(ассоциативность
сложения);
3)
существует такой элемент 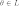 ,
что
,
что 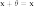 для
любого
для
любого 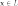 (существование
нейтрального элемента относительно
сложения),
в частности L не
пусто;
(существование
нейтрального элемента относительно
сложения),
в частности L не
пусто;
4)
для любого 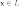 существует
такой элемент
существует
такой элемент 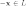 ,
что
,
что 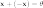 (существование
противоположного элемента относительно
сложения).
(существование
противоположного элемента относительно
сложения).
5)
 (ассоциативность
умножения на скаляр);
(ассоциативность
умножения на скаляр);
6)
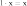 (унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
(унитарность:
умножение на нейтральный (по умножению)
элемент поля P сохраняет вектор).
7)
 (дистрибутивность
умножения на вектор относительно
сложения скаляров);
(дистрибутивность
умножения на вектор относительно
сложения скаляров);
8)
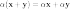 (дистрибутивность
умножения на скаляр относительно
сложения векторов).
(дистрибутивность
умножения на скаляр относительно
сложения векторов).
Пример линейного пространства:
Гильбертово пространство- пространство последовательностей со сходящимся рядом квадратов. Элементами (векторами) такого пространства являются бесконечные числовые последовательности x = (x1, x2,..., xn,...) такие, что ряд x21 + x22 +... + х2n + ... сходится.
24. n-мерное линейное векторное пространство. Размерность и базис векторного пространства. Разложение вектора по системе векторов. Переход к новому базису.
n-мерное векторное пространство – пространство, имеющее n измерений (размерности n). Обычно этот термин применяется к пространству размерностью более трёх. При n=∞ имеем бесконечномерное пространство.
Размерность векторного пространства -максимальное число линейно-независимых векторов в векторном (линейном) пространстве. Если это число конечно, то пространство называется конечномерным (многомерным). В противном случае — бесконечномерным.
Базис векторного пространства - набор из максимального (для данногопространства) числа линейно независимых векторов. Следовательно, все остальные векторы пространства оказываются линейными комбинациями базисных. Если все базисные векторы взаимно ортогональны, а длина каждого из них равна единице, то базис называетсяортонормированным. Единичный базисный вектор называют ортом (обозначается ei, где i — номер координаты).
Каждый вектор пространства может быть представлен в виде линейной комбинации базисных векторов: a = ∑aiei. Коэффициенты разложения ai однозначно определяют вектор a. Поэтому часто говорят, что n-мерный вектор — это упорядоченная совокупность n чисел {ai}. Размерность векторного пространства равна количеству векторов, составляющих его базис.
Разложение вектора по системе векторов:
Пусть 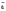 –
произвольный вектор,
–
произвольный вектор, 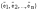 –
произвольная система векторов.
Если выполняется равенство
–
произвольная система векторов.
Если выполняется равенство
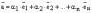 ,
(1)
,
(1)
то
говорят, что вектор
представлен
в виде линейной комбинации
данной системы векторов.
Если данная система векторов
является
базисом векторного пространства,
то равенство (1)
называется разложением вектора
по
базису
. Коэффициенты
линейной комбинации 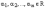 называются
в этом случае координатами
вектора
относительно
базиса
называются
в этом случае координатами
вектора
относительно
базиса 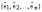 .
.
Переход к новому базису:
Вектор в старом базисе:
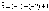 В
новом:
В
новом:
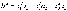 Старые
координаты связаны с новыми
Старые
координаты связаны с новыми
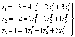 Решив
эту систему с помощью обратной матрицы,
найду координаты вектора
Решив
эту систему с помощью обратной матрицы,
найду координаты вектора 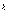 в
новом базисе
в
новом базисе 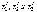 Матрица,
связывающая старые и новые координаты:
Матрица,
связывающая старые и новые координаты:
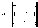 Новые
и старые координаты связаны
отношением:
b=BbI
b
– матрица старых координат;
B –
матрица, связывающая координаты старые
и новые;
BI –
матрица новых координат.
Отсюда:
bI=B-1b
Найду
обратную матрицу B-1.
Новые
и старые координаты связаны
отношением:
b=BbI
b
– матрица старых координат;
B –
матрица, связывающая координаты старые
и новые;
BI –
матрица новых координат.
Отсюда:
bI=B-1b
Найду
обратную матрицу B-1.
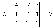 Определитель
≠0 , значит обратная матрица
существует.
Найду алгебраические
дополнения:
Определитель
≠0 , значит обратная матрица
существует.
Найду алгебраические
дополнения: