14. Решение невырожденных систем линейных ур-ий. Теорема Крамера. Привести пример решения слау методом Крамера.

Если определитель системы отличен от нуля, то система называется невырожденной.

Метод Крамера:

Этот метод применятся для решения систем линейных уравнений, в которых число уравнений и число неизвестных совпадают и матрица системы – невырожденная. Справедлива следующая теорема.

ТЕОРЕМА (Крамера). Если в системе линейных уравнений число уравнений и число неизвестных совпадает и , то система совместна и имеет единственное решение, которое может быть найдено по формулам

( ) - формулы Крамера

где 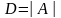, а – определитель, получаемый из определителя 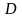заменой его -го столбца на столбец свободных членов.

ПРИМЕР. Решить методом Крамера систему:

Так как число уравнений и число неизвестных в системе совпадают, и определитель матрицы системы , то решение системы может быть найдено по формулам Крамера. Имеем:

, .

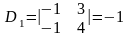Следовательно, , .

Если кол-во ур-ий не равно кол-ву неизвестных, то систему решать методом Гауса.

15. Решение систем лин. ур-ий методом обратной матрицы. Условие существования данного решения. Решение ур-ий вида АХ=В,ХА=В,АХВ=С.

ОПРЕДЕЛЕНИЕ: Обратной к матрице называется матрица, обозначаемая , такая, что .

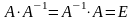СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ

1) Если матрица имеет обратную, то и – квадратные одного порядка.

Действительно, чтобы существовали произведения и необходимо, чтобы матрицы и имели соответственно размеры и . Тогда матрица будет иметь размер , а матрица – размер 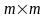. Но для равенства необходимо, чтобы размеры матриц и совпадали, т.е. .

2) Если обратная матрица существует, то она единственная.

Действительно, если предположить, что существует две матрицы и 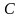обладающие свойством

и ,

то будет существовать и произведение 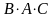, причем

и .

Следовательно, .

3) Если матрица имеет обратную, то определитель матрицы отличен от нуля.

Действительно, так как и для любых квадратных матриц и , то

и, следовательно, и .

Квадратная матрица, определитель которой отличен от нуля, называется невырожденной.

Условие невырожденности матрицы оказалось не только необходимым для существования ее обратной матрицы, но и достаточным.

Условие существования решения методом обратной матрицы.:

Матрица имеет обратную тогда и только тогда, когда ее определитель отличен от нуля. Причем обратная матрица может быть найдена по формуле:

,

где 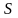– матрица из алгебраических дополнений элементов матрицы , т.е.

.

Матрица называется союзной (или присоединенной, или взаимной) для матрицы .

Решение ур-ий вида АХ = В, ХА = В, АХВ = С

АХ = В, ХА = В, АХВ = С,

где А,В,С — задаваемые матрицы, Х- искомая матрица.

Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.

Например, чтобы найти матрицу из уравнения , необходимо умножить это уравнение на слева.

Тогда:

Следовательно, чтобы найти решение уравнения , нужно найти обратную матрицу и умножить ее на матрицу , стоящие в правой части уравнения.

Аналогично решаются другие уравнения.