1. Метод окаймляющих миноров

Пусть в матрице A найден ненулевой минор n-го порядка M. Рассмотрим все миноры (n + 1)-го порядка, включающие в себя (окаймляющие) минор M; если все они равны нулю, то ранг матрицы равен n. В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется.

2. Метод элементарных преобразований

Ранг матрицы равен числу ненулевых строк в матрице после приведения её к ступенчатой форме при помощи элементарных преобразований над строками матрицы.

Билет 10. Ранг матрицы. Теорема о ранге матрицы.

Рангом матрицы А наз-ся наивысший порядок отличных от нуля миноров этой матрицы.

Теорема о ранге матрицы.  Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А).

Доказательство. Пусть - столбцы, не входящие в БМ и они - максимальная линейно независимая система. Ранг системы столбцов = m (число столбцов входящих в максимальную линейно независимую систему ) по утверждению 1 (если система линейно независима (количество k) и выражается через другую (количество l) то ) . по утверждению 1 и утверждению 2 (все максимальные линейно независимые системы состоят из одного и

того же числа столбцов) и в силу того, что все столбцы линейно выражаются через столбцы максимальной линейно независимой системы

Билет 11. Понятие линейной зависимость и линейной независимости строк (столбцов) матрицы. Теорема о ранге матрицы.

Столбец   называется линейной комбинацией столбцов   одинаковых размеров, если

(3.1)

где   — некоторые числа. В этом случае говорят, что столбец   разложен по столбцам  , а числа  называют коэффициентами разложения. Линейная комбинация   с нулевыми коэффициентами называетсятривиальной.

Если столбцы в (3.1) имеют вид

то матричному равенству (3.1) соответствуют поэлементные равенства, Аналогично формулируется определение линейной комбинации строк одинаковых размеров.

Набор столбцов   одинаковых размеров называется системой столбцов.

Система из   столбцов   называется линейно зависимой, если существуют такие числа  , не все равные нулю одновременно, что

(3.2)

Здесь и далее символом о обозначается нулевой столбец соответствующих размеров.

Система из   столбцов   называется линейно независимой, если равенство (3.2) возможно только при  , т.е. когда линейная комбинация в левой части (3.2) тривиальная. Аналогичные определения формулируются и для строк (матриц-строк).

Замечания 3.1

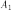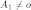1. Один столбец   тоже образует систему: при   — линейно зависимую, а при   линейно независимую.

2. Любая часть системы столбцов называется подсистемой.

Теорема о ранге матрицы. Ранг матрицы А равен максимальному числу линейно независимых столбцов (или равен рангу системы столбцов матрицы А).

Доказательство. Пусть - столбцы, не входящие в БМ и они - максимальная линейно независимая система. ранг системы столбцов = m (число столбцов входящих в максимальную линейно независимую систему ) по утверждению 1 (если система линейно независима (количество k) и выражается через другую (количество l) то ) . по утверждению 1 и утверждению 2 (все максимальные линейно независимые системы состоят из одного и тогоже числа столбцов) и в силу того, что все столбцы линейно выражаются через столбцы максимальной линейно независимой системы