27. Виды систем координат на плоскости. Уравнения связи декартовых и полярных координат. Примеры.

Под системой координат на плоскости понимают способ, позволяющий численно описать положение точки плоскости.

Виды систем: прямоугольная (декартова) система координат и полярная.

П рямоугольная система координат задается двумя взаимно перпендикулярными прямыми — осями, масштабом осей. Одну из осей называют осью абсцисс (осью Ох), другую — осью ординат (осью Оу).(рис.23). Единичные векторы осей обозначают i и j(| i |=| j |=1). Систему координат обозначают Оху, а плоскость, в которой она расположена, называют координатной плоскость. Рассмотрим произвольную т.М пл-ти Оху. Вектор ОМ называется радиусом-вектором т.М. Если ОМ=(x;y), то координаты т. Μ записывают так: М(х;у). Эти два числа x  и  y полностью определяют положение точки на плоскости.

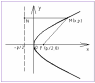
Полярная система координат задается т. О, на­зываемой полюсом, лучом Ор, называемым полярной осью, и единичным вектором e того же направления, что и луч Ор. Возьмем на плоскости т. М, не совпадающую с О. Положение т. М определяется двумя числами: ее расстоянием r от полюса О и углом φ, образован­ным отрезком ОМ с полярной осью (отсчет углов ведется в направлении, противоположном движению часовой стрелки) (см. рис. 24). Числа r и φ называются полярными координатами т. М, пишут М(r; φ), при этом r называют полярным радиусом, φ — полярным углом.

Для получения всех точек плоскости достаточно полярный угол φ ограничить промежутком (-; ] (или 0< φ < 2r), а полярный радиус — [0;∞). В этом случае каждой точке плоскости (кроме О) соответствует единственная пара чисел r и φ, и обратно.

Установим связь между прямоугольными и полярными координатами. Для этого совместим полюс О с началом координат системы Оху, а полярную ось — с положительной полуосью Ох. Пусть x и у — прямоугольные координаты точки М, а r и φ — ее полярные координаты. Из рисунка 25 видно, что прямоугольные координаты точки М выражаются через полярные координаты точки с ледующим образом:

Полярные же координаты т. М выражаются через ее декартовы координаты (тот же рисунок) такими формулами

Определяя величину φ, следует установить (по знакам x и у) четверть, в которой лежит искомый угол, и учитывать, что - < φ< .

28. Прямая на плоскости. Виды задания прямой на плоскости. Взаимное расположение прямых на плоскости.

Общее уравнение прямой на плоскости в декартовых координатах: Ах+Ву+С=0, где A, B и C — произвольные постоянные, причем A и B не равны 0 одновременно

Способы задания прямой: 1)Задание с помощью зависимости у=у(х). 2)Параметрическое задание: х=х(t), у=у(t), где t-параметр. 3)Векторное задание  r=r(t), где t- параметр.

Прямые на плоскости:1) у=kx+b – уравнение прямой с угловым коэффициентом k. 2)общее уравнение прямой Ах+Ву+С=0. 3) уравнение прямой, проходящей через данную точку в данном направлении: y-yo=k(x-xo). 4)уравнение прямой, проходящей через две точки: . Если х1=х2, то урав-е имеет вид х=х1. Если у1=у2 уравнение прямой примет вид у=у1. 5)уравнение прямой в отрезках . 6)уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору А(х-х0)+В(у-у0)=0.

Частные случаи расположения прямой: 1)если прямая проходит через начало координат, то b=0; 2) если прямая параллельна оси Ох, то у=b; 3) если прямая параллельна оси Оу, то х=const.

29.Прямая на плоскости. Угол между прямыми. Условие параллельности и перпендикулярности.

Общее уравнение прямой на плоскости в декартовых координатах: Ах+Ву+С=0, где A, B и C — произвольные постоянные, причем A и B не равны 0 одновременно.

Угол между прямыми можно вычислить:

I. Пусть прямые заданы с помощью ур-ий с угл. коэф.

l1: y=k1x+b1; l2: y=k2x+b2

tg=(k2-k1)/(1+k2*k1) 1) если k1= k2, то прямые параллельны; 2)если k2k1= -1, то прямые перпендикулярны; 3)если k1≠k2, то прямые пересекаются

II. Пусть прямые заданы с помощью общих уравнений:

tg=(А1В2-А2В1)/(А1А2-В1В2)  1)если А1В2= А2В1, то прямые параллельны; 2) если А1/А2= В1/В2=С1/С2, то прямые совпадают; 3) если А1А2+В1В2=0, то прямые перпендикулярны; 4) если А1В2≠А2В1, то прямые пересекаются.

30.Прямая на плоскости. Угол между прямыми. Расстояние от точки до прямой.

Общее уравнение прямой на плоскости в декартовых координатах: Ах+Ву+С=0. Угол между прямыми tg=(А1В2-А2В1)/(А1А2-В1В2)

Уравнение прямой с угловым коэф. у=kx+b. Угол между прямыми tg=(k2-k1)/(1+k2*k1).

Расстоянием от точки до прямой называется перпендикуляр опущенный из этой точки на данную прямую. Пусть точка М₁(х₁, у₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁: .

Либо такая формула

31.Кривые второго порядка. Канонические уравнения, графики, определения.

Кривая называется кривой (линией) второго порядка, если она определяется уравнением второй степени относительно текущих координат х и у, т.е. уравнением вида Аx² + 2Вxy + Сy² + 2Dx + 2Еy + F = 0. К кривым второго порядка относятся: окружность, эллипс, гипербола, парабола.

1) Окружностью радиуса R с центром в т. М0(х0;у0) наз-ся множество всех таких точек пл-ти М, что расстояние М0М всегда одно и то же и равно R. Каноническое уравнение (x – х0)² + (y – у0)² = R²

2) Эллипсом наз-ся множество всех точек на пл-ти, сумма расстояний от каждой из которых до двух данных точек этой пл-ти, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. Канонич.ур-е эллипса

3) Гиперболой наз-ся множество всех точек пл-ти, модуль разности расстояний от каждой до двух данных точек пл-ти, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами. Канонич. ур-е гиперболы:

4) Параболой наз-ся множество всех точек пл-ти, каждая из которых одинаково удалена от данной точки, называемой фокусом и данной прямой, называемой директрисой. Расстояние от фокуса до директрисы наз-ся параметром параболы и обозн-ся р. Канонич. ур-е параболы у²=2рх (парабола симметрична оси Ох)

х²=2ру (симметрична оси Оу)

у²= -2рх (имеет фокус F(р/2;0) и директрису х= -р/2)

х²= -2ру (имеет фокус F(0;р/2) и директрису у= -р/2