
- •1.Матрицы. Основные понятия. Виды матриц.
- •2.Линейные операции над матрицами. Св-ва операций.
- •3.Нелинейные операции над матрицами. Св-ва операций.
- •4. Определители. Основные понятия. Свойства определителей.
- •Свойства определителей
- •5.Вычисление определителей 2-го и 3-го порядков. Св-ва определит.(сумма опред., тождественные преобраз., сумма произвед. Эл-ов строк и столбцов)
- •Свойства определителей
- •6.Определители. Минор. Алгебраическое дополнение. Теорема Лапласа.
- •1. Метод окаймляющих миноров
- •2. Метод элементарных преобразований
- •Билет 11. Понятие линейной зависимость и линейной независимости строк (столбцов) матрицы. Теорема о ранге матрицы.
- •12. Системы линейных алгебраических уравнений (слау). Основные понятия. Матричная форма записи слау.
- •13. Системы лин.Ур-ий. Реш-ие сист. Лин. Ур-ий. Теорема Кронекера-Капелли.
- •14. Решение невырожденных систем линейных ур-ий. Теорема Крамера. Привести пример решения слау методом Крамера.
- •1 6. Решение систем линейных ур-ий методом исключения Гаусса (алгоритм решения, достоинства и недостатки данного метода).
- •Пример расчета межотраслевого баланса
- •22. Векторное произведение. Представление в виде определителя. Ориентация результирующего вектора. Модуль векторного произведения, его геометрический смысл.
- •23.Общее определение линейного пространства. Линейное векторное пространство. Примеры линейных пространств.
- •25. Определение скалярного произведения векторов в n-мерном векторном пространстве, его свойства. Евклидово действительное пространство. Ортогональный и ортонормированный базис в пространстве.
- •26. Собственные векторы матриц. Собственные числа матриц. Характеристическое уравнение. Базис определяемый собственными векторами матрицы.
- •27. Виды систем координат на плоскости. Уравнения связи декартовых и полярных координат. Примеры.
- •28. Прямая на плоскости. Виды задания прямой на плоскости. Взаимное расположение прямых на плоскости.
- •32.Плоскость в трехмерном пространстве. Виды задания пл-тей.
25. Определение скалярного произведения векторов в n-мерном векторном пространстве, его свойства. Евклидово действительное пространство. Ортогональный и ортонормированный базис в пространстве.
Ортогональный базис:
1) Два вектора называются ортогональными (перпендикулярными), если угол между ними прямой.
2) Система векторов называется ортогональной, если все векторы, образующие её попарно ортогональны.
Ортонормированный базис:
1) Система векторов называется ортонормированной, если она ортогональна и длина каждого вектора = 1.
С
калярное
произведение векторов(ab,
(a,b),a*b)–скалярным
произведением ненулевых векторов а
и b
называется число, равное произведению
длин этих векторов на косинус угла
между ними: (a,b)
= |a |
* |b |
* cos = |b|
* проекцию b
на a
= |b|
* проекцию b
на a
Свойства скалярного произведения:
1 ) (a , b) = (b, a)
2 ) (λa, b) = λ (a, b)
3 ) (a, b + c) = (a, b) + ( a , c)
4 ) (a , a) = | a|^2
5 ) (a, b) = 0, когдаa |b
6 )еслиa |b,то (a, b) = 0
Евклидово
пространство - в
изначальном смысле, пространство,
свойства которого описываются аксиомами евклидовой
геометрии.
В этом случае предполагается, что
пространство имеет размерность 3.В
современном понимании, в более общем
смысле, может обозначать один из сходных
и тесно связанных объектов. Обычно n-мерное
евклидово пространство обозначается  ,
хотя часто используется не вполне
приемлемое обозначение
,
хотя часто используется не вполне
приемлемое обозначение  .
.
Конечномерное гильбертово
пространство,
то есть конечномерное вещественное векторное
пространство  с
введённым на нём (положительно
определенным)скалярным
произведением,
порождающим норму:
с
введённым на нём (положительно
определенным)скалярным
произведением,
порождающим норму:
 ,
,
в простейшем случае (евклидова норма):

где  (в
евклидовом пространстве всегда можно
выбрать базис,
в котором верен именно этот простейший
вариант).
(в
евклидовом пространстве всегда можно
выбрать базис,
в котором верен именно этот простейший
вариант).
26. Собственные векторы матриц. Собственные числа матриц. Характеристическое уравнение. Базис определяемый собственными векторами матрицы.
Нахождение
собственных чисел и собственных векторов
матриц: Собственными
числами матрицы  являются
корни уравнения|А-
λE|
= 0и только они.
являются
корни уравнения|А-
λE|
= 0и только они.
Пусть
столбец a -
собственный вектор матрицы  с
собственным числом
с
собственным числом  .
Тогда, по определению,
.
Тогда, по определению,  .
Это равенство можно переписать в видеАа
– л а = 0 .
Так как для единичной матрицы
.
Это равенство можно переписать в видеАа
– л а = 0 .
Так как для единичной матрицы  выполнено
выполнено  ,
то Аa
–λEa
= 0 .
По свойству матричного умножения (A
–λE)a
= Aa–λEa и
предыдущее равенство принимает вид
,
то Аa
–λEa
= 0 .
По свойству матричного умножения (A
–λE)a
= Aa–λEa и
предыдущее равенство принимает вид
|
(A) |
Допустим, что определитель матрицыA – л E отличен от нуля, |A – л E|≠ 0 . Тогда у этой матрицы существует обратная (A – л Е)^-1 . Из равенства (А) получим, что а = (А – л Е)^-1 * 0 = 0 , что противоречит определению собственного вектора. Значит, предположение, что | A – л Е| ≠ 0, неверно, то есть все собственные числа должны являться корнями уравнения|А –л Е| = 0 .
Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A, если Av = λv, где число λ называется собственным значением матрицы A. Таким образом преобразование, которое выполняет матрица A над вектором v, сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v — собственный вектор, то и αv— тоже собственный вектор.

Характеристическое уравнение матрицы— алгебраическое уравнение вида
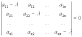 ;
;
определитель, стоящий в левой части Х. у., получается из определителя матрицы А = ||aik||n1 вычитанием величины l из диагональных элементов. Этот определитель представляет собой многочлен относительно Х — характеристический многочлен. В раскрытом виде Х. у. записывается так:
 ,
,
где S1 = a11 + a22 +... ann —
т. н. след матрицы, S2 —
сумма всех главных миноров 2-го порядка,
т. е. миноров вида  (i < k)
и т.д., а Sn —
определитель матрицы А.
Корни Х. у. l1,
l2,...,
ln называются
собственными значениями матрицы А.
У действительной симметричной матрицы,
а также у эрмитовой матрицы все
lk действительны,
у действительной кососимметричной
матрицы все lk чистомнимые
числа; в случае действительной
ортогональной матрицы, а также унитарной
матрицы все |lk|
= 1.
(i < k)
и т.д., а Sn —
определитель матрицы А.
Корни Х. у. l1,
l2,...,
ln называются
собственными значениями матрицы А.
У действительной симметричной матрицы,
а также у эрмитовой матрицы все
lk действительны,
у действительной кососимметричной
матрицы все lk чистомнимые
числа; в случае действительной
ортогональной матрицы, а также унитарной
матрицы все |lk|
= 1.
Базис, определяемый собственными векторами матрицы:

