
- •1. Основные определения
- •Определение электрической и магнитной цепей
- •Электрические и магнитные величины
- •2. Законы (правила) Кирхгофа. Параллельное и последовательное соединение двухполюсников.
- •Ветвь, узел и контур
- •Напряжение участке электрической цепи
- •2.3 Законы Кирхгофа
- •2.4 Параллельное и последовательное соединение двухполюсников
- •3. Методы анализа сложных электрических цепей
- •Анализ сложных цепей с использованием уравнений электрического состояния
- •3.2Анализ сложных цепей с использованием метода наложения.
- •3.3 Анализ сложных цепей с использованием метода узлового напряжения.
- •4. Методы анализа нелинейных электрических цепей при постоянном токе
- •4.1 Статическое и динамическое сопротивления нелинейных резистивных элементов
- •4.2 Расчет нелинейных цепей методом линеаризации
- •4.3 Расчет нелинейных цепей методом пересечения характеристик
- •5. Анализ линейных электрических цепей при переменном токе
- •5.1 Основные параметры, характеризующие синусоидальные токи, эдс и напряжения.
- •Действующее и среднее значения синусоидальных величин
- •5.2 Электрическая цепь переменного тока с резистивным элементом
- •5.3 Электрическая цепь переменного тока с индуктивным элементом
- •5.4 Электрическая цепь переменного тока с резистивным и индуктивным элементами
- •5.5 Электрическая цепь переменного тока с емкостным элементом
- •5.6 Электрическая цепь переменного тока с резистивным и емкостным элементами
- •5.7 Электрическая цепь переменного тока с резистивным, индуктивным и емкостным элементами
- •5.8 Резонанс напряжений и токов в электрических цепях
- •Резонанс напряжений
- •Резонанс токов
- •5.9 Представление синусоидально изменяющихся электрических величин комплексными числами
- •5.10 Анализ и расчет простых электрических цепей переменного тока с помощью комплексных чисел.
- •6. Трехфазные электрические цепи
- •6.1 Трехфазная система электрических цепей. Основные понятия и определения
- •6.2 Способы соединения фаз источника энергии (генератора) и фаз потребителей энергии
- •Способы соединения фаз источника энергии (генератора)
- •Способы соединения фаз нагрузки
- •Магнитные цепи
- •Трансформаторы
Действующее и среднее значения синусоидальных величин
При практическом использовании переменного электрического тока широко применяют действующие значения тока (ЭДС, напряжения). Большинство расчетов проводится с использованием действующих значений величин. Шкалы большинства приборов проградуированы в действующих значениях измеряемых величин и в паспортных данных на электротехнические приборы приводятся действующие значения токов и напряжений.
Действующее значение I переменного тока (ЭДС, напряжения), или действующий ток (ЭДС, напряжение) – это среднее квадратичное значение тока (ЭДС, напряжения) за период Т:
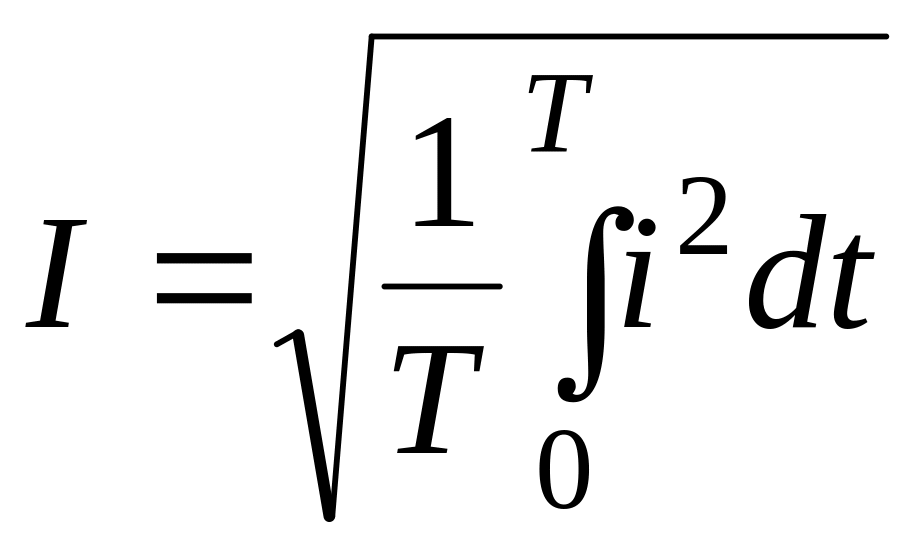 .
(5.3)
.
(5.3)
Действующим значением I переменного тока называется такое значение постоянного тока, при прохождении которого через резистивный элемент, на нем за период Т выделится такое же количество энергии, что и при прохождении переменного тока.
Для синусоидального тока установим соотношение между амплитудным и действующим токам. Для интеграла тока запишем:
![]() .
(5.4)
.
(5.4)
Поскольку
![]() ,
перепишем (5.4) в виде:
,
перепишем (5.4) в виде:
![]() и подставив результат в (5.3) получим:
и подставив результат в (5.3) получим:
![]() .
.
Аналогично
действующие значения ЭДС и напряжения:
![]() и
и
![]() .
.
Таким образом
действующие
значения синусоидальных величин в
![]() раз меньше их амплитудных значений.
раз меньше их амплитудных значений.
В ряде случаев при анализе и расчете процессов в цепях требуется знать средние значения переменных токов (ЭДС, напряжений).
Среднее значение
тока (ЭДС,
напряжения) – это среднее арифметическое
значение тока (ЭДС, напряжения) за
интервал времени. Для синусоидальных
величин в качестве интервала времени
выбирают половину периода, т.е.
![]() ,
т.к. среднее значение синусоидальной
величины за период равно нулю. Среднее
значение синусоидального тока:
,
т.к. среднее значение синусоидальной
величины за период равно нулю. Среднее
значение синусоидального тока:
![]() .
(5.5)
.
(5.5)
Аналогично для
ЭДС и напряжения:
![]() ,
,
![]() .
.
5.2 Электрическая цепь переменного тока с резистивным элементом
Пусть в электрической
цепи с резистивным элементом R
(рис. 5.4) ток изменяется по синусоидальному
закону:
![]() .
Для упрощения начальная фаза тока
принята равной нулю (
.
Для упрощения начальная фаза тока
принята равной нулю (![]() ).
Тогда напряжение на резистивном элементе:
).
Тогда напряжение на резистивном элементе:
![]() .
(5.6)
.
(5.6)
где
![]() – амплитудное значение напряжения на
резисторе.
– амплитудное значение напряжения на
резисторе.
R

i
UR

Рис.5.4
Векторная и угловая диаграммы тока и напряжения на резистивном элементе приведены на рис. 5.5.
 π/2
π/2
Um Um
Im
Im π/2 0 π 2π
Im Um 0 π/2 ωt
Рис. 5.5
Поскольку начальные
фазы тока и напряжения равны нулю, то
разность фаз тока и напряжения на
резистивном элементе равна нулю (![]() )
и следовательно векторы напряжения и
тока совпадают по направлению.
)
и следовательно векторы напряжения и
тока совпадают по направлению.
Мгновенная и средняя мощность в цепи с резистивным элементом
Записав определение
мощности
![]() для мгновенных значений тока и напряжения
и подставив в него значения тока и
напряжения из (5.6) получим:
для мгновенных значений тока и напряжения
и подставив в него значения тока и
напряжения из (5.6) получим:
![]() .
Учитывая, что
.
Учитывая, что
![]() ,
а
,
а
![]() ,
где
,
где
![]() – действующие значения напряжения и
тока, окончательно получим:
– действующие значения напряжения и
тока, окончательно получим:
![]() .
(5.7)
.
(5.7)
Диаграммы тока, напряжения и мощности резистивного элемента приведены на рис. 4.6.
Средняя (активная) мощность, потребляемая резистивным элементом, определяется как произведение действующих значений напряжения и тока:
![]()
 (5.8)
(5.8)

 P
P
U, I, P
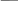




 P=UI
P=UI
 i
i

π/2 π 3π/4 2π ωt

U
Рис. 5.6
