5. Анализ линейных электрических цепей при переменном токе

5.1 Основные параметры, характеризующие синусоидальные токи, эдс и напряжения.

Переменный ток (ЭДС, напряжение) может изменяться во времени как по периодическому, так и по непериодическому закону. Наиболее широко используется периодический ток (ЭДС, напряжение) изменяющийся по синусоидальному закону. Такой ток характеризуется периодом Т – минимальным интервалом времени по истечении которого значения тока повторяются. Период измеряется в секундах. Величина, обратная периоду, т.е. число полных изменений периодической величины за 1 с, называется частотой:

. Частота измеряется в герцах (Гц).

Синусоидальные ток, ЭДС и напряжение могут быть представлены в аналитическом виде:

, , (5.1)

где – мгновенные значения синусоидального тока (ЭДС, напряжения); – амплитудные значения (амплитуда) синусоидального тока (ЭДС, напряжения), т.е. наибольшие из мгновенных значений; – аргумент синусоидальной функции, называемый фазой (тока, ЭДС, напряжения); – угловая частота, характеризующая скорость изменения фазы (тока, ЭДС, напряжения) и измеряющаяся в радианах в секунду (рад/с); – начальная фаза (фаза в момент времени ) синусоидального тока (ЭДС, напряжения), которая является алгебраической величиной и может иметь положительные и отрицательные значения.

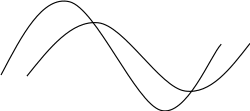
На рис.5.1 приведены графические изображения синусоидальных напряжения и тока, имеющих различные начальные фазы. Начальную фазу синусоиды отсчитывают от нулевой фазы (перехода синусоидальной функции от отрицательных значений к положительным) до начала отсчета времени . Начальная фаза напряжения сдвинута влево от начала отсчета времени и считается положительной . Начальная фаза тока сдвинута вправо от начала отсчета времени и считается отрицательной .

U, i

U_m

I_m U

ωt

ψ_u ψ_i i

T

Рис. 5.1

Алгебраическая величина, равная разности начальных фаз двух синусоидальных функций, называется сдвигом фаз . На рис. 4.1 сдвиг фаз между напряжением и током . Сдвиг фаз может быть как положительным, так и отрицательным. Положительный сдвиг фаз между напряжением и током на рис. 4.1 указывает на то, что напряжение по фазе опережает ток. Временной сдвиг между напряжением и током:

. (5.2)

Векторное изображение синусоидальных электрических величин

При синусоидальном изменении электрической величины неизменной остается ее амплитудное значение. Поэтому синусоидальную функцию можно изобразить вектором, равным амплитуде данной функции, равномерно вращающимся с угловой частотой (скоростью) против часовой стрелки (рис.5.2). Начальное положение вектора (для ) определяется его начальной фазой .

i

I_m ωt I_m

I_m

ωt₃ ψ_i π t₂ t₃ 2π

t₁ ωt

ψ_i I_t2 I_t3

I_m

ωt₃

Рис.5.2

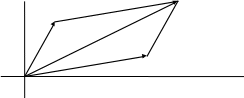
С помощью векторов можно производить геометрическое суммирование синусоидальных электрических величин одной частоты. На рис. 5.3 показаны векторы токов и , а также вектор их геометрической суммы . Углы , и обозначают их начальные фазы. Векторные диаграммы широко используют при анализе процессов в цепях переменного тока.

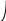
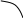
Рис.5.3