24. Кинетическая энергия системы материальных точек. Теорема Кенига

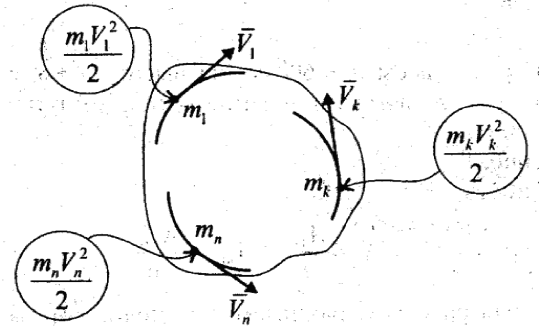
Кинетическая энергия механической системы – арифметическая сумма кинетических энергий всех материальных точек этой системы:

.

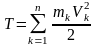Кинетическая энергия системы, состоящей из n связанных между собой тел, равна арифметической сумме кинетических энергий всех тел этой системы:

.

Кинетическая энергия механической системы в общем случае ее движения определяется теоремой Кенига:

Кинетическая энергия механической системы равна сумме кинетической энергии движения системы вместе с центом масс и кинетической энергии системы при ее движении относительно центра масс:

,

где – скорость k-й точки системы относительно центра масс.

25. Кинетическая энергия твердого тела

Рассмотрим вычисление кинетической энергии твердого тела в частных случаях его движения:

1 . Поступательное движение. При поступательном движении тела . В этом случае

.

2 . Вращение тела вокруг неподвижной оси. В этом случае

,

где – момент инерции тела относительно оси вращения.

3. Плоскопараллельное движение.

При плоском движении тела кинетическая энергия складывается из кинетической энергии поступательного движения тела со скоростью центра масс 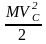и кинетической энергии вращательного движения вокруг оси, проходящей через центр масс, :

.

Плоскопараллельное движение эквивалентно мгновенному вращению вокруг оси, проходящей через МЦС. Поэтому . С учетом этого, получим

,

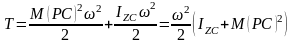где – теорема Гюйгенса-Штейнера. Тогда

.

26. Теорема об изменении кинетической энергии системы

Теорема об изменении кинетической энергии механической системы в дифференциальной форме:

1. Дифференциал кинетической энергии механической системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на эту систему:

,

где – сумма элементарных работ внешних сил, действующих на систему, – сумма элементарных работ внутренних сил.

2. Производная по времени от кинетической энергии системы равна мощности всех внешних и внутренних сил, действующих на эту систему:

.

Теорема об изменении кинетической энергии механической системы в интегральной или конечной форме:

Изменение кинетической энергии механической системы на некотором перемещении равно сумме работ внешних и внутренних сил, действующих на материальные точки системы на этом перемещении:

.

Учитывая, что сумма работ внутренних сил твердого тела на любом перемещении равна нулю, получим

.

Теорему об изменении кинетической энергии применяют в тех случаях, когда движущаяся система является неизменной, т.е. расстояние между точками системы остается неизменным. Частным случаем такой системы является абсолютно твердое тело.

Эту теорему целесообразно применять в тех случаях, когда в число данных и искомых величин входят массы или моменты инерции тел, скорости (линейные или угловые), а силы и моменты пар сил либо постоянны, либо зависят от положения точек тела.

27. Вычисление работы сил, действующих на твердое тело

1. Работа внутренних сил.

Д ля двух k-х точек: , т.к. и .

Элементарная работа всех внутренних сил в твердом теле равна нулю: .

Следовательно, на любом конечном перемещении тела

.

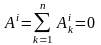2. Работа внешних сил.

а ) Поступательное движение тела:

Элементарная работа k-й силы

.

Для всех сил .

Т.к. при поступательном движении , то

,

где – проекция главного вектора внешних сил на направление перемещения.

Работа сил на конечном перемещении S

.

б) Вращение тела вокруг неподвижной оси.

Э лементарная работа k-й силы

,

где – составляющие силы по естественным осям .

Т.к. , то работа этих сил на перемещении точки приложения силы равна нулю. Тогда

.

Элементарная работа k-й внешней силы равна произведению момента этой силы относительно оси вращения 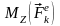на элементарный угол поворота тела вокруг оси.

Элементарная работа всех внешних сил

.

где 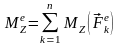– главный момент внешних сил относительно оси.

Работа сил на конечном перемещении

.

Если , то ,

где – конечный угол поворота; , – число оборотов тела вокруг оси.