
- •1.Законы Ньютона
- •2.Дифференциальные уравнения движения материальной точки
- •3.Первая основная задача динамики пункта и ее решение
- •4. Вторая основная задача динамики точки и ее решение
- •5. Виды колебаний материальной точки. Свободные колебания
- •6. Затухающие колебания точки
- •7. Вынужденные колебания точки при отсутствии сопротивления среды
- •8. Вынужденные колебания точки при наличии сопротивления среды
- •9. Дифференциальные уравнения относительного движения точки. Переносная и кориолисова сила инерции
- •10. Некоторые основные понятия динамики системы материальных точек (система материальных точек, связи, силы)
- •11. Масса и центр масс системы материальных точек
- •12. Момент инерции тела. Радиус инерции
- •13. Зависимость между моментами инерции относительно параллельных осей (теорема Гюйгенса-Штейнера)
- •14. Осевые моменты инерции тел простейшей формы
- •15. Теорема о движении центра масс механической системы. Закон сохранения
- •16. Количество движения механической системы. Импульс силы
- •17. Теоремы об изменении количества движения механической системы. Закон сохранения
- •18. Момент количества движения материальной точки и механической системы
- •19. Теорема об изменении главного момента количеств движения системы. Закон сохранения
- •20. Кинетическая интерпретация теоремы моментов (теорема Резаля)
- •21. Две меры механического движения. Кинетическая энергия материальной точки
- •22. Теорема об изменении кинетической энергии материальной точки
- •23. Работа силы. Мощность. Теоремы о работе. Примеры вычисления работы
- •24. Кинетическая энергия системы материальных точек. Теорема Кенига
- •25. Кинетическая энергия твердого тела
- •26. Теорема об изменении кинетической энергии системы
- •27. Вычисление работы сил, действующих на твердое тело
- •28. Элементарная теория гироскопа. Гироскоп с тремя степенями свободы
- •29. Движение тяжелого гироскопа
- •30. Возможные перемещения. Идеальные связи
- •31. Принцип возможных перемещений (принцип Лагранжа)
- •32. Методика применения принципа возможных перемещений
- •33. Понятие о принципе Даламбера. Принцип Даламбера для материальной точки
- •34. Принцип Даламбера для системы материальных точек
- •35. Приведение сил инерции
- •36. Общее уравнение динамики
- •37. Обобщенные координаты. Обобщенные скорости и число степеней свободы механической системы.
- •38. Обобщенные силы и способы их вычисления
- •39. Условия равновесия механической системы в обобщенных координатах
- •41. Уравнения движения механической системы в обобщенных координатах или уравнения Лагранжа второго рода
- •42. Методика применения уравнений Лагранжа второго рода для решения задач
- •43. Понятие о потенциальном (консервативном) силовом поле и потенциальной энергии. Закон сохранения механической энергии
- •44. Уравнения Лагранжа второго рода для консервативных систем
- •45. Понятие об устойчивости равновесия консервативной системы
- •46. Понятие о малых колебаниях механической системы
18. Момент количества движения материальной точки и механической системы
Так
как количество движения
 ,
как и сила
,
является
величиной векторной, то момент количества
движения относительно центра и оси
определяется так же, как момент силы
относительно того же центра и оси.
,
как и сила
,
является
величиной векторной, то момент количества
движения относительно центра и оси
определяется так же, как момент силы
относительно того же центра и оси.
Векторный момент количества движения материальной точки относительно некоторого центра О – вектор, приложенный в этом центре и направленный перпендикулярно плоскости векторов и в ту сторону, откуда движение точки видно против хода часовой стрелки.
Это определение удовлетворяет векторному равенству
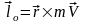 ,
,
где – вектор количества движения материальной точки, – радиус-вектор этой точки относительно центра О.
Алгебраический
момент
количества движения материальной точки
относительно некоторого центра О
– скалярная величина, взятая со знаком
«+» или «-» и равная произведению модуля
количества движения
на расстояние h
(перпендикуляр) от этого центра до линии,
вдоль которой направлен вектор
:
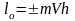 .
.
Моментом
количества движения
(кинетическим моментом) материальной
точки относительно некоторой оси Z
называется скалярная величина
 ,
взятая со знаком «+» или «-» и равная
произведению модуля
,
взятая со знаком «+» или «-» и равная
произведению модуля
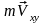 проекции вектора
количества движения на плоскость,
перпендикулярную этой оси, на перпендикуляр
h,
опущенный из точки пересечения оси с
плоскостью на линию, вдоль которой
направлена указанная проекция.
проекции вектора
количества движения на плоскость,
перпендикулярную этой оси, на перпендикуляр
h,
опущенный из точки пересечения оси с
плоскостью на линию, вдоль которой
направлена указанная проекция.
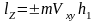 .
.
Правило знаков: смотрим навстречу оси Z
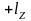 –
при
движении точки против хода часовой
стрелки;
–
при
движении точки против хода часовой
стрелки;
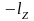 –
то
же по ходу часовой стрелки.
–
то
же по ходу часовой стрелки.
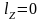 ,
если
,
если
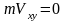 ,
т.е вектор
параллелен
оси ОZ;
,
т.е вектор
параллелен
оси ОZ;
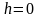 ,
т.е. вектор
пересекает
ось ОZ.
,
т.е. вектор
пересекает
ось ОZ.
Момент количества движения материальной точки относительно оси равен проекции на эту ось момента количества движения материальной точки относительно любого центра, лежащего на этой оси:
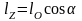 .
.
Для движущейся материальной системы вводится понятие главного момента количеств движения относительно центра О как векторной суммы моментов количеств движения всех точек системы относительно этого центра О:
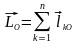 .
.
Вводится и понятие главного момента количеств движения относительно оси – как алгебраической суммы моментов количеств движения точек системы относительно этой оси Z:
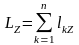 .
.
Зависимость между ними аналогична зависимости между соответствующими главными моментами сил.
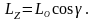
Е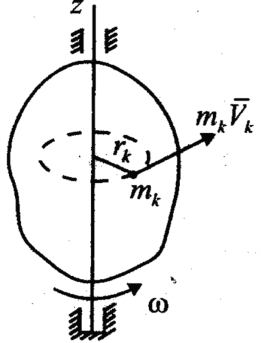 сли
твердое тело (механическая система)
вращается вокруг неподвижной оси Z,
главный момент количеств движения
относительно оси вращения
сли
твердое тело (механическая система)
вращается вокруг неподвижной оси Z,
главный момент количеств движения
относительно оси вращения
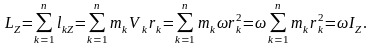
Т.е. равен произведению момента инерции тела относительно оси вращения на угловую скорость
19. Теорема об изменении главного момента количеств движения системы. Закон сохранения
Теорема об изменении кинетического момента в векторной форме формулируется так:
Производная по времени от кинетического момента механической системы относительно данного неподвижного центра О равна главному моменту внешних сил относительно того же центра, т.е.
 .
(3.22.1)
.
(3.22.1)
Теорема об изменении кинетического момента механической системы относительно оси заключается в следующем:
Производная по времени от кинетического момента механической системы относительно данной неподвижной оси равна главному моменту внешних сил относительно этой оси, т.е.
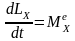 .
.
Законы сохранения кинетического момента механической системы:
1. Если главный момент внешних сил относительно некоторого центра равен нулю, то кинетический момент системы относительно этого центра остается постоянным, т.е.
если
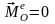 ,
то
,
то
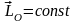 .
.
2. Если главный момент внешних сил относительно некоторой оси равен нулю, то кинетический момент системы относительно этой же оси остается неизменным, т.е.
если
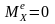 ,
то
,
то
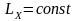 .
.
