15. Теорема о движении центра масс механической системы. Закон сохранения
Теорема о движении центра масс является следствием основных законов Ньютона и формулируется следующим образом:
Центр масс механической системы движется как материальная точка, в которой сосредоточена масса всей системы и к которой приложены все внешние силы, действующие на систему, т.е.
,
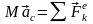(3.18.1)
где
М
– масса системы;
–
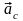ускорение центра масс системы;
–
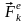геометрическая сумма всех внешних сил,
приложенных к системе, равная главному
вектору внешних сил.
Спроектировав векторное уравнение (3.18.1) на оси прямоугольных декартовых координат, получим
,
,
.
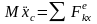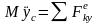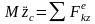(3.18.2)
При решении задач следует иметь в виду, что
,
,
,
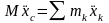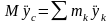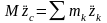где
–
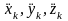проекции абсолютного ускорения точек
системы на оси декартовых координат.
Уравнения (3.18.1) и (3.18.2) описывают поступательное движение твердого тела.
Теорема о движении центра масс позволяет получить важные следствия, которые называются законами сохранения движения центра масс.
1. Если главный вектор внешних сил, приложенных к механической системе, равен нулю, то цент масс движется равномерно и прямолинейно.
2. Если проекция главного вектора внешних сил на какую-либо ось равна нулю, то проекция скорости центра масс на эту ось есть величина постоянная.
Пусть
.
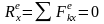Тогда из уравнения (3.18.2) получим, что
,
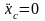откуда
.
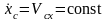В
частности, если в начальный момент
времени
,
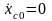то в любой последующий момент
.
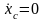В этом случае центр масс системы вдоль
оси 0Х
перемещаться
не будет, т.е.
.
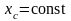16. Количество движения механической системы. Импульс силы
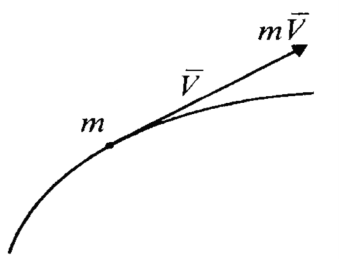
Количество движения материальной точки – векторная мера ее движения, равная произведению массы точки на вектор ее скорости.
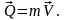
Количеством
движения механической системы
или главный вектор количества движения
– геометрическая сумма количеств
движения всех материальных точек
системы.
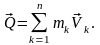(3.19.1)
Преобразуем уравнение (3.19.1):
,
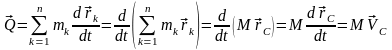где
–
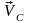скорость центра масс.
Модуль главного вектора количества движения системы определяется через его проекции на оси декартовых координат
.
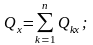
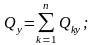
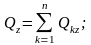
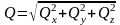Импульс силы – векторная мера действия силы в течение некоторого времени.
Элементарный
импульс
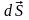силы
–
векторная величина, равная произведению
вектора силы на элементарный промежуток
времени
,
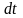т.е.
.
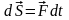Импульс
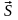силы
за
конечный промежуток времени
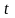равен интегральной сумме соответствующих
элементарных импульсов, т.е.
.
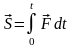(3.19.2)
Выражение (3.19.2) в проекциях на оси координат
.
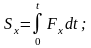
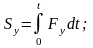
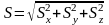Направляющие косинусы определяются по формулам:
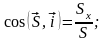
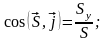
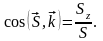
Импульс равнодействующей нескольких сил за некоторый промежуток времени равен геометрической сумме импульсов составляющих сил за этот промежуток времени.
.
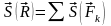17. Теоремы об изменении количества движения механической системы. Закон сохранения
Теорему об изменении количества движения механической системы в дифференциальной форме можно сформулировать двумя способами:
1. Векторная производная по времени от количества движения механической системы равна главному вектору внешних сил, приложенных к этой системе:
,
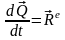т.е. скорость изменения количества движения механической системы равна главному вектору внешних сил.
2. Дифференциал количества движения механической системы равен элементарному импульсу главного вектора внешних сил этой системы:
.
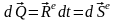Теорема об изменении количества движения механической системы в интегральной форме:
Изменение количества движения механической системы за некоторый промежуток времени равно импульсу вектора внешних сил за тот же промежуток времени, т.е.
.
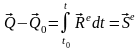(3.20.1)
В проекциях на оси декартовых координат векторное равенство (3.20.1) имеет вид:
.
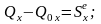
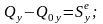
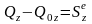Следствие (закон сохранения количества движения механической системы).
1)
Если главный вектор внешних сил равен
нулю, то количество движения системы
остается постоянным по модулю и
направлению, т.е. если
,
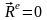то
.
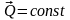2)
Если проекция главного вектора внешних
сил системы на какую-либо ось равна
нулю, то проекция количества движения
системы на эту ось остается постоянной,
т.е. если
,
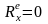то
.