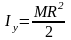- •1.Законы Ньютона
- •2.Дифференциальные уравнения движения материальной точки
- •3.Первая основная задача динамики пункта и ее решение
- •4. Вторая основная задача динамики точки и ее решение
- •5. Виды колебаний материальной точки. Свободные колебания
- •6. Затухающие колебания точки
- •7. Вынужденные колебания точки при отсутствии сопротивления среды
- •8. Вынужденные колебания точки при наличии сопротивления среды
- •9. Дифференциальные уравнения относительного движения точки. Переносная и кориолисова сила инерции
- •10. Некоторые основные понятия динамики системы материальных точек (система материальных точек, связи, силы)
- •11. Масса и центр масс системы материальных точек
- •12. Момент инерции тела. Радиус инерции
- •13. Зависимость между моментами инерции относительно параллельных осей (теорема Гюйгенса-Штейнера)
- •14. Осевые моменты инерции тел простейшей формы
- •15. Теорема о движении центра масс механической системы. Закон сохранения
- •16. Количество движения механической системы. Импульс силы
- •17. Теоремы об изменении количества движения механической системы. Закон сохранения
- •18. Момент количества движения материальной точки и механической системы
- •19. Теорема об изменении главного момента количеств движения системы. Закон сохранения
- •20. Кинетическая интерпретация теоремы моментов (теорема Резаля)
- •21. Две меры механического движения. Кинетическая энергия материальной точки
- •22. Теорема об изменении кинетической энергии материальной точки
- •23. Работа силы. Мощность. Теоремы о работе. Примеры вычисления работы
- •24. Кинетическая энергия системы материальных точек. Теорема Кенига
- •25. Кинетическая энергия твердого тела
- •26. Теорема об изменении кинетической энергии системы
- •27. Вычисление работы сил, действующих на твердое тело
- •28. Элементарная теория гироскопа. Гироскоп с тремя степенями свободы
- •29. Движение тяжелого гироскопа
- •30. Возможные перемещения. Идеальные связи
- •31. Принцип возможных перемещений (принцип Лагранжа)
- •32. Методика применения принципа возможных перемещений
- •33. Понятие о принципе Даламбера. Принцип Даламбера для материальной точки
- •34. Принцип Даламбера для системы материальных точек
- •35. Приведение сил инерции
- •36. Общее уравнение динамики
- •37. Обобщенные координаты. Обобщенные скорости и число степеней свободы механической системы.
- •38. Обобщенные силы и способы их вычисления
- •39. Условия равновесия механической системы в обобщенных координатах
- •41. Уравнения движения механической системы в обобщенных координатах или уравнения Лагранжа второго рода
- •42. Методика применения уравнений Лагранжа второго рода для решения задач
- •43. Понятие о потенциальном (консервативном) силовом поле и потенциальной энергии. Закон сохранения механической энергии
- •44. Уравнения Лагранжа второго рода для консервативных систем
- •45. Понятие об устойчивости равновесия консервативной системы
- •46. Понятие о малых колебаниях механической системы
11. Масса и центр масс системы материальных точек
Рассмотрим механическую систему, состоящую из n материальных точек.
М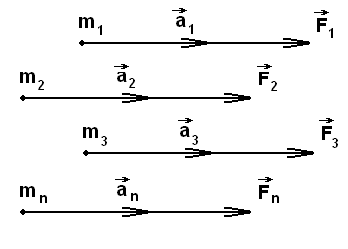 ассой
системы материальных точек называется
физическая величина равная арифметической
сумме масс всех точек, входящих в систему.
ассой
системы материальных точек называется
физическая величина равная арифметической
сумме масс всех точек, входящих в систему.
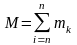
Масса характеризует инертные свойства системы материальных точек при ее постоянном движении.
Центром
масс или центром инерции механической
системы называется геометрическая
точка, радиус-вектор
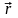 которой
определяется равенством
которой
определяется равенством
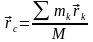 ,
,
где
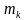 ,
,
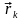 –
соответственно масса и радиус-вектор
k-ой
точки системы.
–
соответственно масса и радиус-вектор
k-ой
точки системы.
Декартовы координаты центра масс определяются формулами:
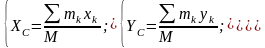
где
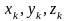 –
координаты k-ой
точки системы.
–
координаты k-ой
точки системы.
Зависимость между скоростью центра масс и скоростями точек механической системы имеет вид:
 .
.
Зависимость между ускорением центра масс и ускорениями точек механической системы выражается соотношением
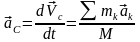 .
.
12. Момент инерции тела. Радиус инерции
При поступательном движении системы мерой ее инерции служит масса, для характеристики инерционных свойств в других случаях движения вводят понятия о моментах инерции системы.
Различают полярные, осевые, планарные и центробежные моменты инерции.
Моментом инерции тела относительно полюса (полярным моментом инерции) называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния этой точки до полюса 0:
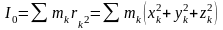
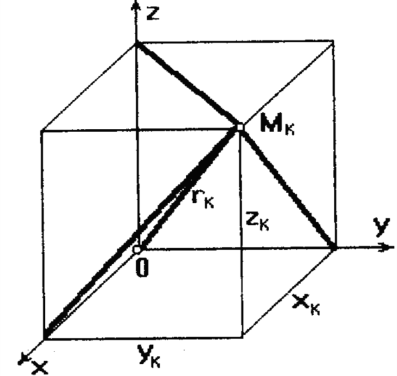 .
.
Моментом инерции тела относительно оси (осевым моментом инерции) называется величина, равная сумме произведений массы каждой точки тела на квадрат расстояния этой точки до оси:
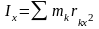 ;
;
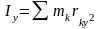 ;
;
 или
или
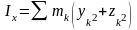 ;
; ;
;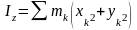
Моментом инерции тела относительно плоскости (планарным моментом инерции) называется величина равная сумме произведений масс каждой точки тела на квадрат расстояния этой точки до плоскости:
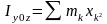 ;
;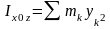 ;
;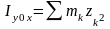 .
.
Моментом инерции тела относительно пары координат осей (x,y) (центробежным моментом инерции) называется величина равная сумме произведений масс всех точек тела на их координаты в этих осях:
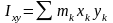 ;
;
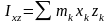 ;
;
 .
.
В
отличие от остальных моментов инерции
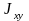 ,
,
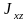 ,
,
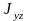 могут быть как положительными, так и
отрицательными, а все остальные только
положительными.
могут быть как положительными, так и
отрицательными, а все остальные только
положительными.
Между перечисленными моментами инерции тела существует определенная зависимость:
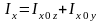 ;
;
 ;
;
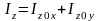 ;
;

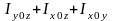 .
.
13. Зависимость между моментами инерции относительно параллельных осей (теорема Гюйгенса-Штейнера)
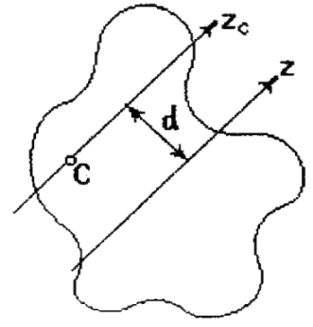
Существует простая связь между моментами инерции твердого тола относительно параллельных осей, одна из которых проходит через центр масс. Эта связь устанавливается теоремой Гюйгенса-Штейнера: момент инерции твердого тела относительно некоторой оси равен моменту инерции тела относительно параллельной оси, проходящей через центр масс, сложенному с произведением массы тела на квадрат расстояния между осями:
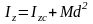 .
.
14. Осевые моменты инерции тел простейшей формы
-
№ п/п
Название твердого тела
Вид
твердого тела
Моменты инерции
1
Материальная точка массы m
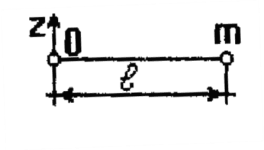
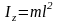
2
Тонкое однородное кольцо
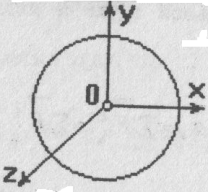

3
Круглый однородный диск массы М и радиуса R
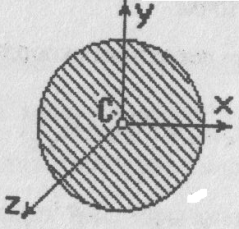
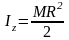 ,
,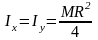
4
Тонкий однородный стержень массы М и длины l
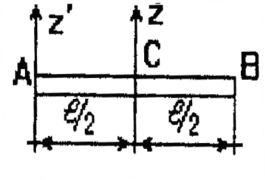
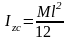 ,
,
5
Однородная прямоугольная пластина массы М
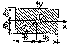
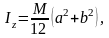
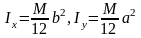
6
Круглый цилиндр массы М, радиуса R и высотой l
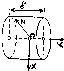
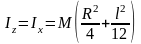 ,
,