39. Условия равновесия механической системы в обобщенных координатах

Выразим возможную работу сил, приложенных к механической системе, в обобщенных координатах:

,

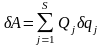где – обобщенные силы, соответствующие обобщенным координатам ; – вариации обобщенных координат.

Принцип возможных перемещений в обобщенных силах можно записать

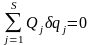. (3.43.1)

Из выражения (3.43.1) следует условие равновесия механической системы в обобщенных силах

, ,

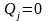т.е. для равновесия механической системы с идеальными, стационарными, двусторонними и голономными связями необходимо и достаточно, чтобы обобщенные силы по всем обобщенным координатам были равны нулю.

Для равновесия консервативных систем

, .

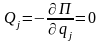41. Уравнения движения механической системы в обобщенных координатах или уравнения Лагранжа второго рода

Уравнения Лагранжа второго рода – это дифференциальные уравнения движения механической системы в обобщенных координатах.

Для системы с S степенями свободы эти уравнения имеют вид

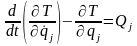, . (3.44.1)

Разность полной производной по времени от частной производной от кинетической энергии системы по обобщенной скорости и частной производной от кинетической энергии по обобщенной координате равна обобщенной силе.

Если механическая система движется в потенциальном силовом поле, то , и уравнение Лагранжа второго рода принимают вид

, .

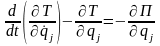42. Методика применения уравнений Лагранжа второго рода для решения задач

На основании уравнений (3.44.1) разработана универсальная методика решения задач динамики. Она заключается в следующем:

1) Устанавливаем число степеней свободы механической системы (S).

2) Вводим в систему S обобщенных координат.

3) Находим S обобщенных сил, соответствующих введенным координатам.

4) Составляем выражения кинетической энергии механической системы в виде функции обобщенных координат и обобщенных скоростей.

5) Составляем уравнения Лагранжа 2-го рода.

В результате получаем S обыкновенных дифференциальных уравнений второго порядка относительных обобщенных координат.

6) Решаем эти уравнения алгебраически и находим ускорения точек системы, или же интегрируем полученные уравнения, и определяем кинематические уравнения движения точек в обобщенных координатах.

43. Понятие о потенциальном (консервативном) силовом поле и потенциальной энергии. Закон сохранения механической энергии

Силовым полем называется физическое пространство, удовлетворяющее условию, при котором на точки механической системы, находящейся в этом пространстве, действуют силы, зависящие только от положения этих точек или от положения точек и времени.

Силовое поле, силы которого не зависят от времени, называются стационарным

Будем рассматривать стационарные силовые поля, когда проекции силы являются функциями только координат, т.е.

, , .

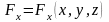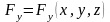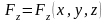Силовое стационарное поле называется потенциальным, если работа сил поля, действующих на механическую систему, не зависит от формы траектории ее точек и определяется только их начальным и конечным положениями.

Эти силы называются силами, имеющими потенциал, или консервативными силами.

Приведенное условие выполняется, если существует однозначная функция координат

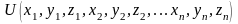
называемая силовой функцией поля, частные производные от которой по координатам любой точки 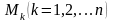равны проекциям приложенной к этой точке силы на соответствующие оси:

, , .

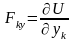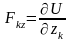Элементарная работа сил потенциального поля равна полному дифференциалу силовой функции, т.е.

.

Работа сил поля на конечном перемещении механической системы из положения (1) в положение (2)

,

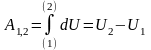т.е. работа сил, действующих на точки механической системы в потенциальном поле, равна разности значений силовой функции в конечном и начальном положениях системы и не зависит от формы траекторий точек этой системы.

Отсюда следует, что на замкнутом пути работа силы, имеющей потенциал, равна нулю. ,

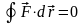где 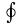– криволинейный интеграл, взятый по замкнутому контуру.

Потенциальная энергия материальной точки определяется работой, которую совершает сила консервативного поля при перемещении этой точки из данного положения в нулевое.

Потенциальная энергия зависит от положения точки:

.

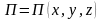Потенциальная энергия системы материальных точек является функцией от координат всех n точек системы, т.е.

.

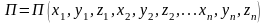Из определения потенциальной энергии системы следует, что в нулевом положении ее значение равно нулю: .

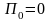Работа сил, приложенных к точкам механической системы, на любом ее перемещении равна разности значений потенциальной энергии в начальном и конечном положениях системы.

.

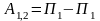Элементарная работа потенциальной силы равна полному дифференциалу потенциальной энергии, взятой с обратным знаком:

.

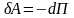Получим

, , .

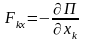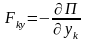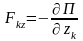Г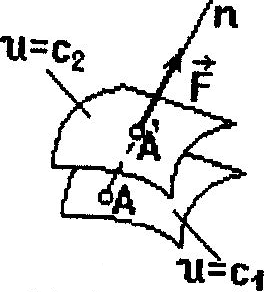 еометрическое место точек, в которых потенциальная энергия сохраняет постоянное значение, называется поверхностью равного потенциала или эквипотенциальной поверхностью: .

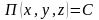Сила действующая в потенциальном поле, направлена по нормали к эквипотенциальной поверхности в данной точке в сторону убывания потенциальной энергии.

Закон сохранения механической энергии материальной точки и механической системы заключается в следующем:

Если на материальную точку или механическую систему действуют только консервативные силы, то в любом положении точки или системы сумма кинетической и потенциальной энергий остается величиной постоянной.