31. Принцип возможных перемещений (принцип Лагранжа)

Пусть материальная система находится в равновесии. Силы, действующие на каждую ее точку, уравновешиваются. Если 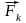– равнодействующая всех активных сил, приложенных к k-той точке, а – реакция связей этой точки, то .

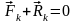Дадим системе какое-нибудь возможное перемещение. Все точки ее получат перемещения δS₁, δS₂, δS₃,…, δS_k.

Затем вычислим работу всех сил на этих перемещениях.

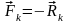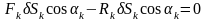Так как силы, приложенные к каждой точке уравновешиваются и , то сумма работ этих сил на перемещении δS_k будет равна нулю: . Значит и сумма работ всех сил, приложенных ко всем точкам, будет равна нулю .

Если связи идеальные, то вторая сумма всегда равна нулю. Значит,

(3.35.1)

Этот результат, уравнение работ, называют общим уравнением статики.

При равновесии материальной системы с идеальными и стационарными связями сумма работ всех активных, задаваемых, сил на любом возможном перемещении системы из положения равновесия равна нулю.

Если у системы есть неидеальные связи, например, с трением, или упругие, вроде пружины, то в уравнение работ надо добавить возможную работу реакций этих связей.

Принцип возможных перемещений можно записать в другой форме.

Если возможные перемещения точек определить с помощью возможных скоростей: 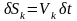, где время 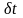- произвольная бесконечно малая величина, то уравнение работ запишется так 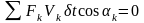, а, поделив его на δt получим , (3.35.2)

где 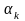– углы между направлениями сил и направлениями векторов возможных скоростей точек приложения сил.

Равенство (3.35.2)можно назвать принципом возможных скоростей, уравнением мощностей. Оно иногда бывает более удобным, так как используются конечные величины скоростей, а не бесконечно малые перемещения.

32. Методика применения принципа возможных перемещений

В уравнения работ, выражающие принцип возможных перемещений, не входят реакции идеальных связей, но тем не менее, с помощью принципа возможных перемещений достаточно просто решаются задачи определения реакций связей. В этом случае используется принцип освобождаемости от связей: отбрасываем связь, реакцию которой требуется определить, и действие связи заменяем реакцией связи, которая переходит в число задаваемых сил. При этом система, освобожденная от одной связи, получает одну степень свободы. Далее системе сообщаем возможное перемещение, соответствующее этой степени свободы, и составляем уравнения работ. В уравнения работ входят задаваемые силы и реакция отброшенной связи.

Для определения реакций других связей следует отбросить снова только одну связь, т.е. сообщить системе одну степень свободы.

33. Понятие о принципе Даламбера. Принцип Даламбера для материальной точки

Уравнение движения материальной точки массы m относительно инерциальной системы отсчета под действием приложенных активных сил и реакций связей имеет вид: ,

где – равнодействующая активных сил; – равнодействующая реакций связей; – ускорение точки относительно инерциальной системы отсчета.

Получим .

Введем обозначение . Вектор , равный по модулю произведению массы точки на ее ускорение и направленный противоположно вектору ускорения, называется силой инерции.

Тогда получим, что . (3.37.1)

Полученное соотношение выражает принцип Даламбера для материальной точки: геометрическая сумма всех приложенных к материальной точке сил и силы инерции этой точки равна нулю.

При этом следует иметь ввиду, что к материальной точке приложены только силы и , т.е. активная сила и реакция связи. Сила инерции к точке не приложена. Она является силой действия материальной точки на тело, сообщающее ей ускорение, и приложена к этому телу.

Если точка совершает прямолинейное движение, то вектор силы инерции материальной точки направлен противоположно вектору .

Если точка движется по заданной криволинейной траектории, то ее ускорение можно определить как сумму нормального и тангенциального ускорений, т.е. . Тогда силу инерции также необходимо представить в виде двух составляющих: нормальной и тангенциальной . Численно , а .

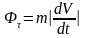Из векторного равенства (3.37.1) в проекциях на оси координат получаем три уравнения: (3.37.2)

Равенства (3.37.2) представляют собой уравнение движения материальной точки, записанное в форме условия равновесия сил. Такой метод решения задач динамики, основанный на сведении ее к соответствующей задаче статики посредством условного присоединения силы инерции к силам, приложенным к материальной точке, называется методом кинетостатики.