18. Локальные свойства функций имеющих предел.

Определение 1. Пусть функция определена на множестве и – некоторое его подмножество ( ). Говорят, что функция ограничена (соотв., ограничена сверху или снизу) на множестве , если его образ есть ограниченное (соотв., ограниченное сверху или снизу) множество.Теорема 1 (о локальной ограниченности). Пусть функция определена на множестве и - точка сгущения этого множества. Тогда если существует предел , то существует такая окрестность точки , что функция ограничена на множестве .Ниже знак числа обозначается через .Теорема 2 (о стабилизации знака). Пусть функция определена на множестве и - точка сгущения этого множества. Тогда если существует отличный от нуля предел , то в некоторой проколотой окрестности точки функция имеет тот же знак, что и этот предел: точнее, существует такая окрестность точки , что

(1)

19. Теорема о пределе суперпозиции.

Теорема (о пределе суперпозиции). Пусть функция определена на множестве , – точка сгущения множества и существует предел

.

(1)

Пусть, кроме того, функция определена на множестве , – точка сгущения множества и существует предел

.

(2)

Тогда, если

,

(3)

то на множестве имеет смысл суперпозиция и существует предел

.

(4)

23.Символы о-малое и о-большое, эквивалентные б.М. И б.Б.

Пусть функции и определены на множестве и – точка сгущения множества . Пусть также в некоторой проколотой окрестности точки функция отлична от нуля (точнее, ). Там где это ниже необходимо по смыслу, будем также считать, что в той же проколотой окрестности отлична от нуля и функция .

Определения: 1. Если ,то говорят, что функция есть о-малое от функции при , и пишут при . 2. Если функция ограничена в некоторой проколотой окрестности точки , т.е. если она ограничена на множестве , то говорят, что функция есть о-большое от функции при , и пишут

при . Говорят, что функции и асимптотически равны при , если

.Если бесконечно малые(большие) при функции и асимптотически равны, то говорят, что они эквивалентны при , при этом пишут ~ ( ).Если бесконечно большие при функции и асимптотически равны при , то говорят, что они эквивалентны при .

Теорема: Пусть и – бесконечно малые(большие) при функции, причем ~ , а ~ при . Тогда если

,то и .

24. Замечательные пределы

(первый замечательный предел), (1)т.е., что

~ ( ).Так как функция – четная, то то достаточно найти правосторонний ее предел в точке . Пусть . , , ,

при этом ясно, что .Поэтому

и, следовательно, Таким образом, если будет доказано, что ,то будет доказано и (1). Используя левое из неравенств (2) получим ,а так как ,то из этих неравенств в силу принципа двух милиционеров получим (3). Итак равенство (1) установлено.Как следствие (1) и (3) имеем В свою очередь из (1) и (4) следует что Таким образом, ~ , а ~ при .

Второй замечательный предел и его следствия. (1) .Покажем, что (8) Действительно, так как ,то для любой последовательности натуральных чисел такой, что имеем (9)Но для любой последовательности вещественных чисел .

где , и, следовательно, .

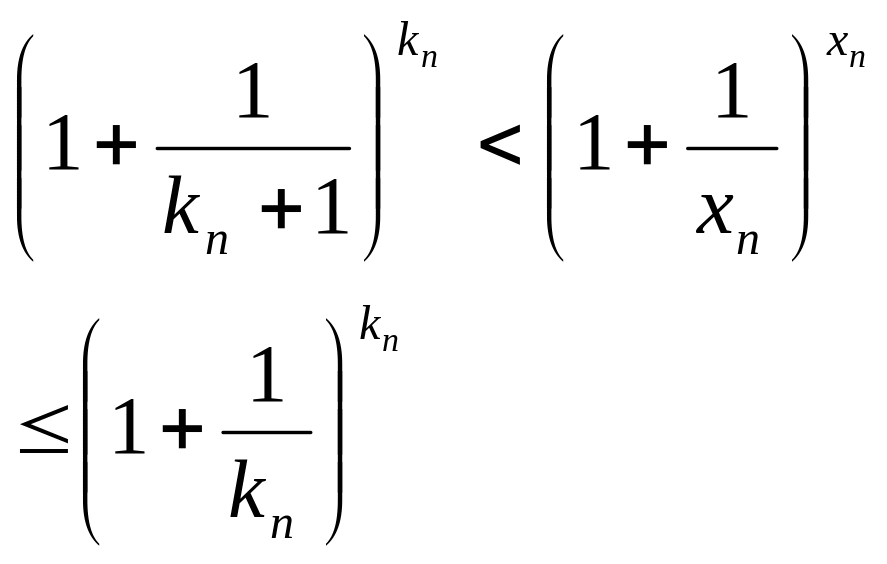Поэтому, если , то и в силу (9) и принципа двух милиционеров, для любой последовательности вещественных чисел , такой, что имеем также .

По определению предела в смысле Гейне это и означает, что справедливо равенство (8). Используя его и теорему о пределе суперпозиции легко убедиться также и в том, что (10)