20. Коэффициент сопряженности Чупрова и коэффициент Крамера, их применение
Коэффициент Чупрова измеряет взаимосвязь качественных неальтернативных признаков, измеренных по номинальной шкале. Подсчитывается по формуле:
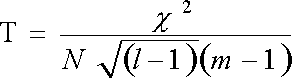
хи
– квадрат, коэффициент квадратической
сопряженности
l, m - число граф и строк в составленной таблице сопряженности признаков
N - общее число объектов в изучаемой совокупности
Коэффициент Крамера подсчитывается для неальтернативных признаков, измеренных по номинальной шкале, по формуле:
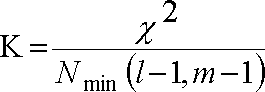
- хи – квадрат, коэффициент квадратический сопряженности
¯минимальное
из чисел в таблице ( l-1,
m
– 1)
χ-квадрат – коэффициент квадратической сопряженности используется для установления факта существования взаимосвязи признаков, измеренных по номинальной шкале, и при подсчете коэффициентов Чупрова и Крамера. Его формула:
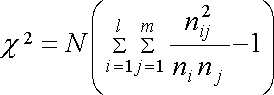
N - итоговая сумма всех значений признаков в таблице сопряженности
- значение признаков в одной из клеток таблицы
- сумма значений признаков в одной из строк таблицы (например, первой)
- сумма значений признака в первой графе таблицы.
21. Среднее арифметическое простое и взвешенное, особенности применения
Наиболее распространенным видом средних величин является средняя арифметическая, которая в зависимости от характера имеющихся данных может быть простой или взвешенной.
Средняя арифметическая простая применяется, когда значение вариантов встречается по одному числу раз.
Средняя арифметическая взбешенная применяется, когда отдельное значение признака повторяется неодинаковое количество раз, т.е. она используется в расчетах средней по 2 сгруппированным данным или вариационным рядам, которые могут быть дискретными и интервальными.
При расчете средней по интервальному вариационному ряду для выполнения необходимых вычислений переходят о интервалов к их серединам.
22. Коэффициенты связи для дихотомических таблиц
При сравнении двух переменных, измеренных в дихотомической шкале, мерой корреляционной связи служит так называемый коэффициент φ. Коэффициент фи представляет собой коэффициент корреляции для дихотомических данных.
Величина коэффициента φ лежит в интервале между +1 и -1и его знак для интерпретации результатов не имеет значения.
Он может быть как положительным и отрицательным, характеризуя направление связи двух дихотомически измеренных признаков. Коэффициент φ можно вычислить методом кодирования, а также используя так называемую четырехпольную таблицу, или таблицу сопряженности.
Для применения коэффициента корреляции φ необходимо соблюдать следующие условия:
1. Сравниваемые признаки должны быть измерены в дихотомической шкале.
2. Число варьирующих признаков в сравниваемых переменных X
и Y должно быть одинаковым.
необходимо соблюдать следующие условия:
1. Сравниваемые признаки должны быть измерены в разных шкалах: одна X – в дихотомической шкале; другая Y – в шкале интервалов или отношений.
2. Переменная Y имеет нормальный закон распределения.
3. Число варьирующих признаков в сравниваемых переменных X
и Y должно быть одинаковым.
Основное назначение корреляционного анализа это выявление связи между переменными.
Мерой связи являются коэффициенты корреляции.
Выбор коэффициента корреляции напрямую зависит от типа шкалы, в которой измерены переменные, числа варьирующих признаков в сравниваемых переменных и распределения переменных.
Наличие корреляции двух переменных еще не означает что между ними существует причинная связь.