4.4.3.Интегральные оценки качества

Отклонение регулируемой величины от установившегося значения переходного процесса и время этого процесса можно охарактеризовать одним числом. Для этого применяются интегральные оценки качества переходного процесса.

Применяются интегральные оценки качества относительно задающего воздействия и относительно возмущения.

Линейная интегральная оценка

Ч исленно она равна площади, ограниченной кривой отклонения x(t) и выражается через изображение по Лапласу X(s) отклонения x(t).

x(t)=y₀+y(t).

.

Линейная интегральная оценка применяется только при монотонном переходном процессе. При колебательном процессе суммарная площадь, ограниченная кривой x(t) , не оценивает качество процесса.

Применяются также линейные интегральные оценки более общего вида

.

Может быть применена интегральная оценка .

Квадратичная интегральная оценка

.

Может применяться для оценки как монотонных, так и колебательных переходных процессов.

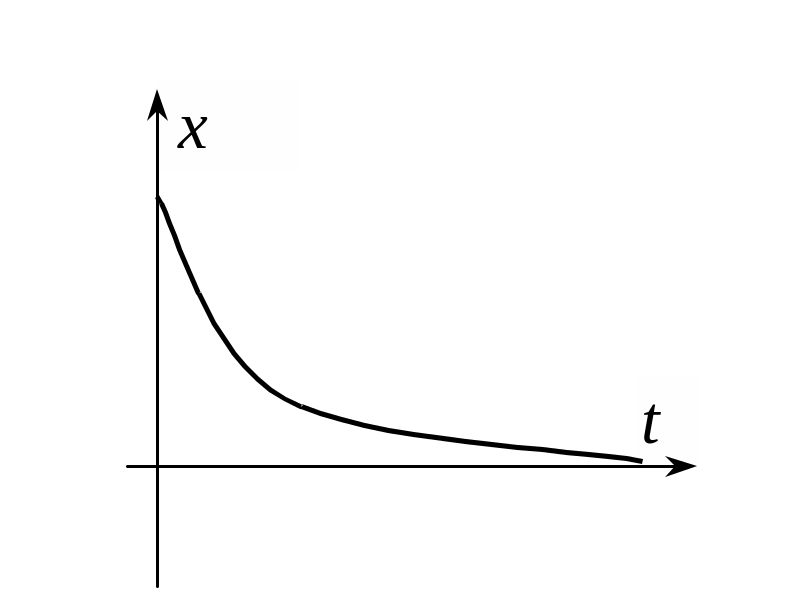
Если выбирать параметры системы исходя из минимума квадратичной интегральной оценки , то переходный процесс может оказаться сильно колебательным. Данный факт ограничивает использование квадратичных интегральных оценок при анализе и синтезе систем автоматического управления.

Улучшенная квадратичная интегральная оценка

.

Здесь Т- некоторая постоянная. Данная формула учитывает и изменение ошибки.

Чем меньше значение , тем меньше отклонение переходной характеристики от экспоненты с постоянной времени Т, называемой экстремалью:

При инженерных расчетах применяют и еще более сложные интегральные оценки, например

,

Интегральная оценка характеризует приближение переходной характеристики системы к экстремали, определяемой дифференциальным уравнением , где и .

Существуют специальные методики выбора параметров системы исходя из минимума интегральной оценки. Решение данной задачи возможно с помощью численных методов параметрической оптимизации.

4.4.4.Оценка качества переходного процесса по расположению нулей и полюсов передаточной функции

Переходная характеристика системы зависит от значения нулей и полюсов ее передаточной функции. Эту зависимость можно использовать для оценки качества переходной характеристики.

В простейшем случае передаточная функция имеет вид

; .

В этом случае переходная характеристика зависит только от полюсов передаточной функции. Корень, ближайший к мнимой оси - доминирующий корень. Может быть и пара доминирующих корней (если они комплексные сопряженные).

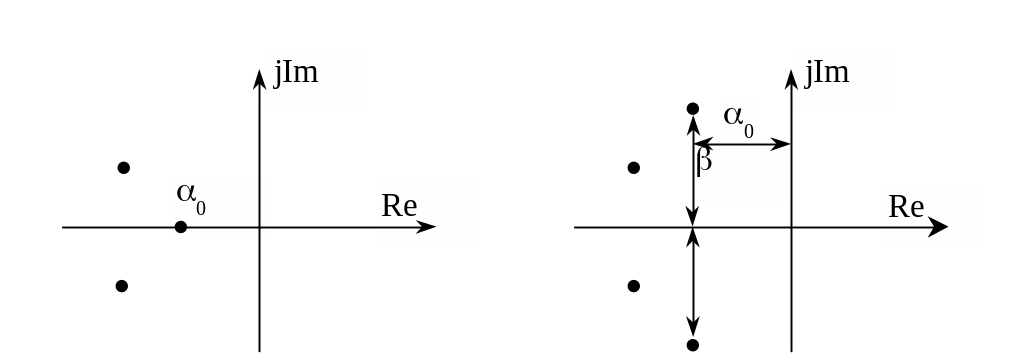
Расстояние доминирующих корней до мнимой оси - ₀, - степень устойчивости системы. Степень устойчивости позволяет определить приближенно время переходного процесса.

Время переходного процесса (при = 5 % ) . Степень устойчивости не следует путать с запасом устойчивости.

Второй параметр, который определяется по плоскости корней - степень колебательности.

.

По величине степени колебательности можно приближенно определить значение перерегулирования переходной характеристики (когда комплексные корни являются доминирующими)

.

Степень колебательности связана также с затуханием переходной характеристики и логарифмическим декрементом затухания следующими формулами: ; ; .

Для оценки влияния нулей (числителя передаточной функции) на качество переходной характеристики передаточную функцию приведем к виду: .

Тогда при ступенчатом входном сигнале имеем

.

а ℒ^-1(y(s))=  ℒ^-1(y_i(s))= .

Если (на данную составляющую нули передаточной функции не влияют), тогда ℒ^-1 ℒ^-1 . Для получения остальных составляющих переходной характеристики необходимо продифференцировать необходимое количество раз и сложить с соответствующими коэффициентами.