3.3.Частотный критерий устойчивости Найквиста

Частотный критерий Найквиста дает возможность определить устойчивость замкнутой системы по АФЧХ ее разомкнутой цепи (разомкнутой системы) . Ниже показано, как определяется передаточная функция разомкнутой системы для случая единичной и неединичной обратной связи.

Следовательно, об устойчивости замкнутой системы с передаточной функцией будем судить по передаточной функции разомкнутой системы , а именно по поведению годографа .

Рассмотрим вспомогательную передаточную функцию

, где обозначено .

Пусть порядок полинома равен n и порядок полинома , причем (в основном так и бывает). Тогда порядок полинома также будет равен n. Различают три возможных ситуации:

1. не содержит правых или нулевых корней, то есть разомкнутая система устойчива.

2. имеет хотя бы один правый корень, следовательно, система в разомкнутом состоянии неустойчива.

3. Все корни левые, но есть и корни на мнимой оси (нейтральная система).

Задача. Определить условия, при которых в замкнутом состоянии система будет устойчива в каждом из трех случаев.

Случай 1. Число правых корней равно 0. Все корни - левые. Разомкнутая система устойчива.

. Для устойчивости замкнутой системы (это наше требование) необходимо, что все корни полинома - левые, то есть .

Применим к принцип аргумента. При изменении от 0 до изменение величины фазового сдвига составляет (в соответствии с правилами деления комплексных чисел):

.

При устойчивой замкнутой системе приращение .

Получили кривую , не охватывающую начало координат:

Если учесть, что , следовательно , или . Таким образом в плоскости получаем:

Точка ( ) на плоскости преобразовалась в точку ( ) на плоскости .

Вывод. Для устойчивости замкнутой системы, устойчивой в разомкнутом состоянии необходимо и достаточно, чтобы годограф АФЧХ разомкнутой системы при изменении от 0 до не охватывал критическую точку с координатой ( ).

На рисунке приведены годографы разомкнутых систем, устойчивых и в замкнутом состоянии.

Характеристики, обозначенные цифрами 1 и 2, соответствуют системам, устойчивым как в разомкнутом, так и в замкнутом состоянии. Для этих систем уменьшение коэффициента усиления отодвигает характеристику от опасной зоны. Характеристика 3 - условно устойчивая система. В условно устойчивой системе уменьшение коэффициента усиления может привести к неустойчивости замкнутой системы.

На следующем рисунке приведен годограф системы, неустойчивой в замкнутом состоянии.

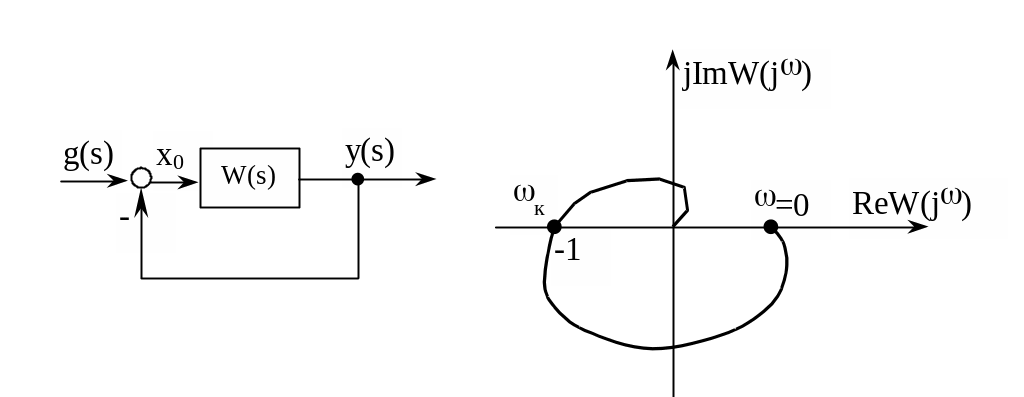
При выходной сигнал отстает от сигнала на входе системы на 180⁰, то есть находится с ним в противофазе. Если =1 (как на рисунке), то при замыкании системы с ООС сигнал x₀, равный алгебраической сумме q и y, не будет ни усиливаться, ни ослабляться. Система будет находиться на границе устойчивости.

Если , то сигнал будет циклически усиливаться. Система становится неустойчивой, даже если снять входной сигнал.

Случай 2. Система в разомкнутом состоянии неустойчива.

Полином имеет m₁ правых корней, n-m₁ - левых. На основании принципа аргумента:

.

Следовательно, для устойчивости замкнутой системы, неустойчивой в разомкнутом состоянии, необходимо и достаточно, чтобы годограф АФЧХ разомкнутой системы при изменении  от 0 до , двигаясь в положительном направлении (против часовой стрелки), раз охватил критическую точку .

Случай 3. В разомкнутом состоянии имеются корни на мнимой оси (нулевые корни).

Передаточная функция разомкнутой системы причем , или . Пусть r =1. Если нулевой корень сдвинуть влево на малую величину , тогда передаточная функция примет вид , а частотная характеристика будет определяться выражением . Дальнейшие рассуждения при получении критерия устойчивости базируются на рассмотренном выше случае 1:

Начальный радиус точки при есть . Если устремить , то начальное значение АФЧХ также изменится: . Следовательно, предельное стягивание корня на свое исходное положение обеспечивает увеличение начального радиуса до , но интегрирующее звено обеспечивает сдвиг по фазе на угол -90⁰.

Вывод. Для устойчивости замкнутой системы, имеющем в разомкнутом состоянии все левые точки, а также 1 или несколько нулевых корней, необходимо и достаточно, чтобы при изменении  от 0 до критическая точка не охватывалась годографом АФЧХ разомкнутой системы вместе с ее дополнением.

Дополнением является дуга с , повернутая от оси вещественных корней на угол .