24. Система случайных величин. Свойства распределения двумерного случайного вектора
В практических применениях ТВ часто приходится сталкиваться с задачами, в которых результат опыта описывается не одной СВ, а двумя или более СВ, образующими систему или комплекс СВ. Например, точка попадания снаряда определяется двумя СВ: абсциссой и ординатой. При стрельбе группой из n-выстрелов совокупность точек попадания на плоскости может рассматриваться как система 2n случайных величин: n абсцисс и n ординат точек попадания.
Пусть
имеется упорядоченная система n
СВ
.
Будем называть ее случайным вектором
и обозначать
,
где
- i-ая
случайная координата вектора
.
Чтобы
задать случайный вектор, надо указать
все те значения, которые он может
принимать, и соответствующие вероятности,
т.е. вероятности, с которыми эти значения
принимаются. Универсальным способом
задания случайного вектора является
задание его функции распределения,
которая определяется равенством
.
В
двумерном случае
– это вероятность попадания случайной
точки
в заштрихованную область
Y
y M(x,y)
0 x X
Остановимся
на двумерном случае. При этом пусть
,
.
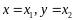Св-ва ф-ции
распределения случайного вектора
аналогичны св-вам ф-ции распределения
СВ:
1. 
;
2. 
-
неубывающая функция по каждой из
переменных;
3. 
,
4.
25. Функция распределения дискретного двумерного случайного вектора
Пусть
распределение вектора
- дискретное, и X
может принимать значения
,
а
-
.
Тогда все возможные ситуации отражаются
в таблице:
Здесь
,
–
это вероятность того, что случайный
вектор
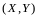примет
значение
,
- вероятность того, что X
примет значение
независимо от значений
Y.
А
,
- вероятность , с которой Y
примет значение
независимо от значений
СВ X.
Функциия
распределения вектора
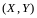определяется равенством
где
суммирование распространяется на все
i,
для которых
,
а
принимает все такие значения, для которых
.