14. Закон распределения случайной величины

Рассмотрим дискретную случайную величину X с возможными значениями . X может принимать любое из этих значений с некоторой вероятностью. В результате опыта произойдет одно событие из полной группы событий . Вероятности этих событий обозначим буквой p с соответствующими индексами –

.

Т.к. эти несовместные события образуют полную группу, то .

Эта суммарная вероятность каким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана с вероятностной точки зрения, если мы зададим это распределение, т.е. укажем, какой вероятностью обладает каждое из событий . Этим мы установим закон распределения случайной величины.

Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

Формой задания закона распределения является таблица

Такую таблицу наз. рядом распределения случайной величины X.

Графическое изображение ряда распределения наз. многоугольником или полигоном

p_i

x₁ x₂ x₃ … x_n x_i

15. Функция распределения случайной величины

Непрерывная СВ имеет бесчисленное множество возможных значений, сплошь заполняющих некоторый промежуток. Для нее не существует ряда распределения, как он существует для дискретной СВ. Но различные области возможных значений этой непрерывной СВ не является одинаково вероятными, и для непрерывной величины существует распределение вероятностей, хотя и не в том смысле, как для дискретной.

Для количественной характеристики этого распределения вероятностей удобно воспользоваться не вероятностью события X=x, а вероятностью события X<x, где x – некоторая текущая переменная.

Вероятность этого события есть некоторая функция от x. Эта функция наз. функцией распределения СВ X и обозначается , .

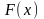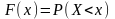Функцию распределения часто наз. интегральной функцией распределения. Функция распределения является универсальной характеристикой СВ. Она существует как для дискретных, так и для непрерывных СВ. Функция распределения полностью характеризует СВ с вероятностной точки зрения, т. е. является одной из форм закона распределения.

16. Общие свойства функции распределения св

Сформулируем общие свойства функции распределения:

1. - неубывающая функция, т.е. при , ;

2. ;

3. .

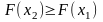Проиллюстрируем эти свойства геометрически. Будем рассматривать СВ 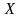как случайную точку на числовой оси.

Тогда есть вероятность того, что случайная точка в результате опыта попадет левее точки .

Будем смещать х вправо по числовой оси. Очевидно, при этом вероятность того, что попадет левее , не может уменьшаться; следовательно, с возрастанием убывать не может.

Неограниченно перемещаем точку влево по оси. При этом попадание случайной точки Х левее х становится невозможным событием. Естественно полагать, что вероятность этого события  0, т.е. .

Аналогично перемещая точку вправо, убеждаемся, что , т. к. событие становится в пределе достоверным.

То, что – монотонно неубывающая функция на всей числовой прямой, можно показать следующим образом: пусть 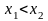. Рассмотрим событие = ( ) и = . , . Применим теорему сложения для несовместных событий и :

или ,

т.е. , т.к. .

Из полученного равенства имеем: .

Построим график функции распределения – это график неубывающей функции, значения которой начинаются от 0 и доходят до 1, причем в отдельных точках функция может иметь разрывы.

F(X)

1

0 X

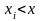Зная ряд распределения случайной величины легко построить функцию распределения этой величины. Действительно, , где неравенство под знаком суммы указывает, что суммирование распространяется на все те значения , которые меньше .

Функция распределения любой дискретной величины есть разрывная ступенчатая функция, разрывы которой происходят в точках, соответствующих возможным значениям случайной величины.

По мере увеличения числа возможных значений случайной величины и уменьшения интервалов между ними число разрывов становится больше, а сами разрывы (скачки) меньше; ступенчатая кривая становится более плавной; случайная величина приближается к непрерывной случайной величине, а ее функция распределения - к непрерывной функции.

На практике обычно функция распределения для непрерывной случайной величины представляет собой функцию, непрерывную во всех точках.

----------------------