
- •1. Событие. Классификация событий
- •2. Вероятность события. Свойства вероятности. Классическая вероятность
- •3. Статистическое определение вероятности
- •4. Геометрическая вероятность
- •5. Задача о встрече
- •6. Действия над событиями
- •7. Теорема сложения вероятностей
- •8. Теорема умножения вероятностей
- •9. Условная вероятность события
- •10. Следствия из теоремы умножения вероятностей
- •11. Формула полной вероятности
- •12. Теорема гипотез (формула Байеса)
- •13. Дискретные и непрерывные случайные величины
- •14. Закон распределения случайной величины
- •15. Функция распределения случайной величины
- •16. Общие свойства функции распределения св
- •17. Плотность распределения случайной величины
- •18. Основные свойства плотности распределения
- •19. Математическое ожидание и его свойства
- •20. Математическое ожидание непрерывной случайной величины
- •21. Мода и медиана
- •22. Дисперсия случайной величины
- •23. Свойства дисперсии
- •24. Система случайных величин. Свойства распределения двумерного случайного вектора
- •25. Функция распределения дискретного двумерного случайного вектора
- •26. Функция и плотность распределения непрерывного двумерного случайного вектора
- •27. Условные законы распределения. Зависимые и независимые случайные величины
- •28. Функция одной дискретной св
- •29. Функция одной непрерывной св
- •30. Корреляционный момент случайных величин X и y и его свойства
- •31. Коэффициент корреляции и его свойства
- •32. Формула Бернулли
- •33. Наивероятнейшее число наступления события
- •34. Асимптотические формулы вычисления вероятностей
- •35. Биномиальный закон распределения
- •36. Закон распределения Пуассона
- •37. Равномерный закон распределения
- •38. Показательный закон распределения
- •39. Нормальный закон распределения
- •40. Математическое ожидание нормального закона распределения
- •41. Дисперсия нормального закона распределения
- •42. Функция Лапласа и ее связь с функцией распределения нормальной случайной величины
- •43. Правило 3σ
- •44. Неравенство Маркова
- •45. Неравенство Чебышева
- •46. Теорема Чебышева
- •47. Теорема Бернулли
- •48. Теорема Ляпунова
- •49. Интегральная теорема Лапласа
- •50. Виды статистических наблюдений
- •51. Виды измерений
- •52. Методы ранжирования
- •53. Группировка и табулирование количественных данных (дискретные и непрерывные вариационные ряды, кумулятивные ряды)
- •54. Графическое изображение вариационных рядов
- •55. Показатели центра распределения (мода, медиана, среднее арифметическое, среднее гармоническое, среднее геометрическое)
- •56. Показатели вариации (размах, лимиты, среднее линейное отклонение, дисперсия, стандартное отклонение)
- •57. Ассиметрия и эксцесс
- •Плосковершинный островершинный полигон
- •58. Оценка показателей альтернативного признака
29. Функция одной непрерывной св
Пусть
X
- непрерывная СВ с плотностью распределения
.
Пусть имеется монотонно возрастающая
на множестве значений СВ X
функция
 (
- непрерывно дифференцируемая и
(
- непрерывно дифференцируемая и
 ).
Если множество значений
).
Если множество значений
 и
и
 и
и
 ,то
функция распределения
,то
функция распределения

 .
.
Здесь
 – есть плотность распределения СВ
.
– есть плотность распределения СВ
.
Для

 (
( -
функция, обратная к
-
функция, обратная к
 на сегменте
на сегменте
 ).
Отсюда
).
Отсюда


Если
- монотонно убывающая функция, то для
функция распределения имеет вид
 ,
а плотность -
,
а плотность -

30. Корреляционный момент случайных величин X и y и его свойства
Пусть
имеется случайный вектор
,
распределение которого известно, т. е.
известна таблица или плотность
распределения
 .
Тогда можно найти
.
Тогда можно найти
 ,
,
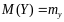 .
По известному закону распределения
можно найти также дисперсии составляющих
вектор
.
Пусть
.
По известному закону распределения
можно найти также дисперсии составляющих
вектор
.
Пусть
 и
и
 .
Однако математические ожидания и
дисперсии СВ X
и Y
недостаточно полно характеризуют
случайный вектор
,
т. к. не выражают степень зависимости
составляющих вектора. Эту роль выполняют
корреляционный момент и коэффициент
корреляции.
.
Однако математические ожидания и
дисперсии СВ X
и Y
недостаточно полно характеризуют
случайный вектор
,
т. к. не выражают степень зависимости
составляющих вектора. Эту роль выполняют
корреляционный момент и коэффициент
корреляции.
Корреляционным
моментом
 случайных величин X
и Y
наз. математическое ожидание произведения
отклонений этих СВ от своих математических
ожиданий:
случайных величин X
и Y
наз. математическое ожидание произведения
отклонений этих СВ от своих математических
ожиданий:
 .
.
Если
распределение дискретное, то
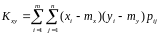 .
.
При
непрерывном распределении
 .
.
Корреляционный момент обладает следующими свойствами:
 – свойство
симметричности.
– свойство
симметричности.
Если
 и
независимые случайные величины, то
и
независимые случайные величины, то
Обратное,
вообще говоря, не имеет места. Если
 ,
то в этом случае величины X
и Y
наз. некоррелированными.
,
то в этом случае величины X
и Y
наз. некоррелированными.
 .
.
 ;
;


 =
= =
= =
=

31. Коэффициент корреляции и его свойства
 -
Корреляционный
момент
-
Корреляционный
момент
Если
отклонения случайных величин от их мат.
ожиданий заменить их нормированными
отклонениями, то получим безмерную
величину - коэффициент
линейной корреляции:

Свойства коэффициента линейной корреляции вытекают из свойств корреляционного момента:
 ;
; ;
; ;
;Если X и Y– независимые СВ, то
 ;
;Если
 , то между
X
и Y
существует линейная зависимость.
, то между
X
и Y
существует линейная зависимость.
Доказательство
проведем для случая
 :
:


Получили, что математическое ожидание неотрицательной величины равно нулю, сама эта величина - тождественный нуль:
 ,
,
что и требовалось доказать.
32. Формула Бернулли
Пусть
некоторый опыт воспроизводится
раз и каждый раз событие A
может наступать с одной и той же
вероятностью p
и не наступает
с вероятностью q=1-p,
независимо от результатов предыдущих
опытов. В этом случае говорят о повторных
независимых испытаниях. При этом событие
A
может наступать 0, 1, 2, … ,
,
… ,
раз. Число наступлений события – это
СВ. Найдем вероятность, с которой событие
A
наступит
раз. Эту вероятность обычно обозначают
символом
 .
Интересующее нас событие – наступление
A
m
раз в n
испытаниях, можно разбить на частные
случаи, каждый из которых определяется
номерами тех испытаний, в которых
наступает A.
Пусть
.
Интересующее нас событие – наступление
A
m
раз в n
испытаниях, можно разбить на частные
случаи, каждый из которых определяется
номерами тех испытаний, в которых
наступает A.
Пусть
 - это
наступление A
в i-ом
испытании. Набор таких i
определяет отдельный случай. Например,
(
- это
наступление A
в i-ом
испытании. Набор таких i
определяет отдельный случай. Например,
( ,
, ,…,
,…, )-
это случай, когда A
наступило в
-ом
испытании, затем
-ом
и т.д., во всех же остальных испытаниях
A
не наступило. Всех случаев будет столько,
сколькими способами мы можем выбрать
m
натуральных чисел из n
(1,2,3,…, n),
т. е. число всех случаев – это число
сочетаний из n
элементов по m
-
)-
это случай, когда A
наступило в
-ом
испытании, затем
-ом
и т.д., во всех же остальных испытаниях
A
не наступило. Всех случаев будет столько,
сколькими способами мы можем выбрать
m
натуральных чисел из n
(1,2,3,…, n),
т. е. число всех случаев – это число
сочетаний из n
элементов по m
- .
.
Найдем
вероятность отдельного случая. Чтобы
он наступил, должны наступить события
 и не наступить события
и не наступить события
 ,
где j
пробегает те числа из 1,2,3,…, n,
которые отличны от
,
,…,
.
Так как все указанные события независимы
и операция умножения событий коммутативна,
то вероятность отдельного случая
,
где j
пробегает те числа из 1,2,3,…, n,
которые отличны от
,
,…,
.
Так как все указанные события независимы
и операция умножения событий коммутативна,
то вероятность отдельного случая




где
 .
.
Мы
видим, что все частные случаи равновозможны,
поэтому, применяя теорему сложения для
несовместных событий, получаем
 - формула Бернулли.
- формула Бернулли.
