20. Математическое ожидание непрерывной случайной величины

Пусть Х– непрерывная СВ, которая принимает значения на [a,b].Тогда плотность распределения Х вне [a,b] равна 0. Разобьем [a,b] на n частей точками

. Тогда получим отрезки , , … , , … , . По теореме о среднем имеем

Здесь - плотность распределения X, 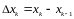, . Рассмотрим дискретную СВ 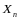, которая принимает значения 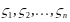с вероятностями . Так как ,

,то СВ определена корректно. .

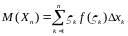Это интегральная сумма для непрерывной функции на [a,b]. Пусть . Тогда дискретная величина 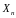будет все менее и менее отличаться от непрерывной случайной величины X, а в пределе она становится непрерывной. Поэтому естественно за математическое ожидание непрерывной величины X взять предел математического ожидания , если последний существует.

Так как -непрерывная функция, то

Аналогично, если _х принимает значения на всей числовой прямой, то

21. Мода и медиана

Модой случайной величины наз. ее наиболее вероятное значение. Термин “наиболее вероятное значение”, строго говоря, применим к дискретной СВ; для непрерывной СВ модой является то значение, в котором плотность максимальна. Обозначается буквой .

Pi f(x)

дискретная непрерывная

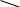
0 0 x

Медианой СВ Х наз. такое ее значение 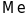, для которого справедливо тождество

т.е. одинаково вероятно, окажется ли случайная величина меньше или больше .

Геометрически медиана - это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.

х

22. Дисперсия случайной величины

Математическое ожидание СВ характеризует ее в среднем – это центр ее распределения.

Дисперсия СВ есть характеристика рассеивания, т. е. расбросанности значений случайной величины около ее математического ожидания.

Дисперсия случайной величины – это математическое ожидание квадрата отклонения СВ от ее математического ожидания .

Если - дискретная случайная величина, заданная рядом распределения

то Если X- непрерывная случайная величина с плотностью распределения , то .

Дисперсия как мера рассеивания значений случайной величины обладает тем недостатком, что ее размерность не совпадает с размерностью случайной величины (размерность дисперсии – это квадрат размерности случайной величины).

Поэтому вводится еще одна мера рассеивания с размерностью, совпадающей с размерностью случайной величины. Это среднее квадратичное отклонение, которое определяется как корень квадратный из дисперсии. Среднее квадратичное отклонение обозначается символом: 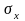или ,

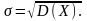
23. Свойства дисперсии

1. Дисперсия постоянной величины равна нулю. .

2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат

= = =

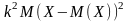3. Дисперсия алгебраической суммы двух независимых СВ равна сумме их дисперсий, то есть Здесь было использовано свойство математического ожидания: если X и Y – независимые случайные величины, то .

4. Упрощенное правило вычисления дисперсии: дисперсия СВ равна разности между математическим ожиданием квадрата СВ и квадратом ее математического ожидания .