11. Формула полной вероятности

Следствием обеих теорем - теоремы сложения и умножения - является так наз. формула полной вероятности.

Пусть требуется определить вероятность некоторого события A, которое может произойти вместе с одним из событий , образующих полную группу несовместных событий. Будем наз. эти события гипотезами.

Докажем, что в этом случае , (*)

т. е. вероятность события вычисляется как сумма произведений вероятности любой гипотезы на вероятность события при этой гипотезе.

Формула (*) носит название формулы полной вероятности.

Доказательство. Так как гипотезы образуют полную группу событий, то событие может появиться только в комбинации с одной из этих гипотез .

Т. к. гипотезы несовместны, то и комбинации - также несовместны. Покажем это - . Применяя к ним теорему сложения, получим

.

Применяя к событию теорему умножения, получим

, что и требовалось доказать.

Пример. На фабрике, изготовляющей болты, первая машина производит 30% , вторая- 25% , третья- 45% всех изделий. Брак в их продукции составляет соответственно 2% , 1% и 3% . Найти вероятность того, что случайно выбранный болт оказался дефектным.

Решение. Обозначим через A событие, состоящее в том, что случайно выбранный болт – дефектный, а через – события, состоящие в том, что этот болт произведен соответственно 1-ой, 2-ой и 3-ей машинами. Из условия задачи следует, что , , ;

, , .

По формуле полной вероятности получаем, что =0.3·0.02+0.25·0.01+0.45·0.3=0.022.

12. Теорема гипотез (формула Байеса)

Следствием теоремы умножения и формулы полной вероятности является так наз. теорема гипотез, или формула Байеса. Поставим следующую задачу.

Имеется полная группа несовместных гипотез . Вероятности этих гипотез до опыта известны и равны соответственно . Произведен опыт, в результате которого появилось событие A. Как следует изменить вероятности гипотез в связи с появлением этого события?

Здесь, по существу, речь идет о том, чтобы найти условную вероятность для каждой гипотезы.

Из теоремы умножения имеем:

или, отбрасывая левую часть,

откуда ,

Выражая Р(А) с помощью формулы полной вероятности, имеем

, - формула Байеса

Пример. Два стрелка независимо один от другого стреляют по одной мишени, делая каждый по одному выстрелу. Вероятность попадания в мишень для первого стрелка 0,8, для второго  0,4. После стрельбы по мишени обнаружена одна пробоина. Найти вероятность того, что эта пробоина принадлежит первому стрелку.

Решение. До опыта возможны следующие гипотезы:

 ни первый, ни второй не попадут;

 оба попадут;

 первый попадет, второй  нет;

 первый не попадет, второй попадет.

Вероятность этих гипотез:

=0,20,6=0,12; =0,32; 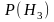=0,80,6=0,48; =0,20,4=0,08.

Условные вероятности наблюденного события при этих гипотезах:

; ; ; .

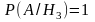После опыта невозможные гипотезы  и .

^.

13. Дискретные и непрерывные случайные величины

Случайной величиной наз. величина, которая в результате опыта может принять то или иное значение, причем не известно заранее, какое именно. Различают СВ дискретного и непрерывного типа. Возможные значения дискретной СВ могут быть заранее перечислены. Возможные значения непрерывной СВ не могут быть заранее перечислены и заполняют некоторый промежуток сплошь.

Примеры дискретных случайных величин:

• число появлений герба при 3-х бросаниях монеты: 0,1,2,3;

• число отказавших элементов в приборе, состоящем из пяти элементов  0,1,2,3,4,5;

• число попаданий в самолет, достаточное для вывода его из строя  1,2,3,…, ,…;

Примеры непрерывных случайных величин:

• абсцисса (ордината) точки попадания при выстреле;

• расстояние от точки попадания до центра мишени;

• время безотказной работы радиолампы.

Будем обозначать случайные величины большими буквами X,Y,…, а их возможные значения  соответствующими малыми буквами. Например, Х  число попаданий при 3-х выстрелах; возможные значения - .

Рассмотрим дискретную случайную величину X с возможными значениями . X может принимать любое из этих значений с некоторой вероятностью. В результате опыта произойдет одно событие из полной группы событий . Вероятности этих событий обозначим буквой p с соответствующими индексами –

.

Т.к. эти несовместные события образуют полную группу, то .