4. Геометрическая вероятность

Классическое определение вероятности предполагает, что число элементарных исходов конечно. На практике часто встречаются опыты, число исходов которых неограниченно. Применение классической вероятности к таким явлениям невозможно. Для этого вводят понятие геометрическая вероятность – вероятность попадания точки в область.

Обозначим меру области g (длину, площадь, объем) через mes g, а меру области G – через mes G (mes первые три буквы французского слова , что значит мера); обозначим буквой событие “попадания брошенной точки в область g, содержащейся в области G.” Вероятность попадания в область g точки, брошенной в область G, определяется формулой:

– это и есть геометрическая вероятность.

Пример. Точка брошена на отрезок единичной длины. С какой вероятностью расстояние от этой точки до концов отрезка ?

Решение. .

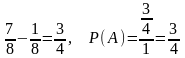5. Задача о встрече

Два студента договорились о встрече в некоторый промежуток времени [0,T], причем каждый из них приходит к месту встречи случайным образом и ждет другого не более τ минут. Найти вероятность встречи студентов.

П усть х и у – моменты прихода студентов к месту встречи. Областью равновозможных значений х и у является квадрат площадью . Встреча произойдет, если . Этому неравенству удовлетворяют точки, лежащие в заштрихованной полосе. Площадь полосы . Тогда

.

6. Действия над событиями

Суммой, или объединением, двух событий называется событие, состоящее в появлении хотя бы одного из них. Сумма событий и обозначается как 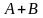или .

Аналогично определяется и обозначается сумма событий – то есть событие, состоящее в появлении хотя бы одного из них. Сумму событий обозначают так: А₁+А₂+…+А_n= или А₁ А₂…А_n=

Произведением или пересечением двух событий называется событие, состоящее в одновременном их появлении.

Произведение событий А и В обозначается через или . Аналогично определяется произведение n событий. Произведение n событий обозначают: А₁А₂…А_n= А_i или А₁А₂…А_n=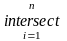 A_i

Операции объединения и пересечения событий обладают некоторыми свойствами, аналогичными операциям умножения и сложения.

Эти операции коммутативны: A 

ассоциативны:(C=C)=C

C=C)=C)

дистрибутивны: С=(АС)С).

Разностью событий и наз. событие C, которое означает, что наступает событие A и не происходит событие B. Разность и обозначается так: 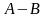или .

7. Теорема сложения вероятностей

Теорема сложения :

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, т.е. .

Докажем теорему сложения вероятностей для схемы n – случаев. Пусть все исходы опыта сведены к совокупности случаев, которые мы изобразим в виде n точек:

m ~ A k ~ B

…………………… …………….

n

из этих n случаев – m благоприятны А, а k – благоприятны В. Тогда . Т. к. события А и В несовместны, то нет таких случаев, которые благоприятны. А и В одновременно. Следовательно, событию А + В благоприятны m + k случаев и , тогда

Обобщим теорему на случай трех событий.A+B=D _=> .

Методом полной индукции теорема обобщается на случай n несовместных событий .

Следствие 1. Если события А₁, А₂, ... А_n образуют полную группу несовместных событий, то сумма их вероятностей равна 1, т.е. .

Доказательство. Так как ; образуют полную группу событий, то появление хотя бы одного из них – достоверное событие: .

Так как – несовместные события, то к ним применима теорема сложения вероятностей, т. е. .

С ледствие 2. Сумма вероятностей противоположных событий равна 1:

Доказательство.

В случае, когда события и совместны, вероятность суммы этих событий выражается формулой: .

В справедливости этой формулы убеждает следующий рисунок

А налогично вероятность суммы трех совместных событий вычисляем по формуле Методом полной индукции можно доказать общую формулу для вероятности суммы любого числа совместных событий: