33. Сравнение бесконечно малых.
Две б.м.ф. сравниваются между собой с помощью их отношения:
1.
если
,
то
и
называются бесконечно
малыми одного порядка.
2.
если
то
называется бесконечно
малой более высокого порядка, чем
.
3.
если
то
называется
бесконечно
малой более низкого порядка, чем
.
4.
если
не существует, то
и
называются несравнимыми
бесконечно малыми.
Таковы
же правила сравнения б.м.ф. при
и
.
Эквивалентные бесконечно малые:
Sinx |
x,
при |
ex - 1 |
x, |
tgx |
x, |
ax - 1 |
x*lna, |
arcsinx |
x, |
ln(1+x) |
x, |
arctgx |
x, |
loga(1+x) |
x*logae |
1-cosx |
|
(1+x)k - 1 |
k*x, k>0, |
,
34. Теоремы о пределах.
Теорема:
если существует
и
и они равны между собой, то существует
=
.
Теорема:
если
,
,
то =>
1)
2)
3)
Примечание 1: 1-е и 2-е свойства распространяются на любое конечное число слагаемых или сомножителей, однако число слагаемых и сомножителей не может быть .
Примечание
2:
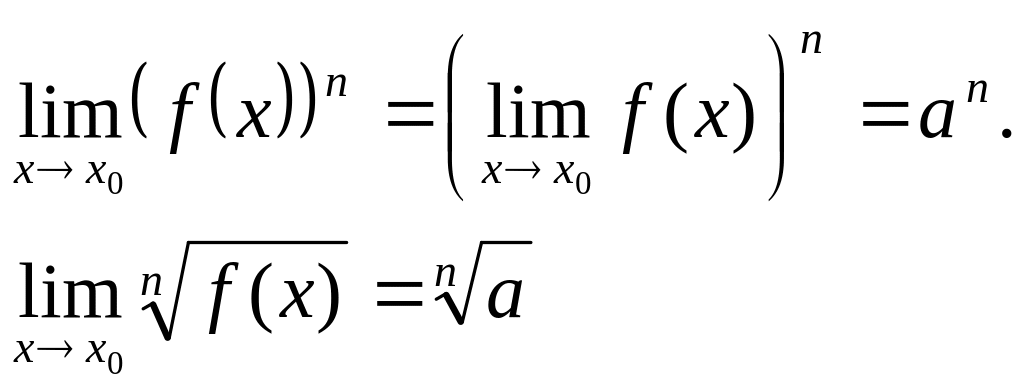
Теорема: если , то функция g(x) = f(x) – a является б.м. при .
Следствие: если => в окрестности т. х0 g(x) + а = f(x), где g(x)- б.м. при .
Теорема:
если
и
существуют конечные пределы, когда
,
=>
.
Теорема
(о сжатой переменной):
если
и
существуют конечные пределы
=>
существует:
.
Теорема (о пределе сложной функции):
Пусть:
х0,
,
U=f(x),
.
Сама теорема:
Если
задана сложная функция,
и
существуют конечные пределы
и
,
то
35. Первый замечательный предел.
При
вычислении пределов выражений, содержащих
тригонометрические функции, часто
используют предел
называемый
первым
замечательным пределом.
Читается: предел отноешния синуса к его аргументу равен единице, когда аргумент стремится к нулю.
Доказательство:
Возьмем
круг радиуса 1, обозначим радианную
меру угла МОВ через х. пусть 0<x<
.
На рисунке
,
дуга МВ численно равна центральному
углу х,
.
Очевидно, имеем
.
На основании соответствующих формул
геометрии получаем
.
Разделим неравенство на
>0,
Получим 1<
Так
как
,
то по признаку ( о пределе промежуточной
функции) существования пределов
.
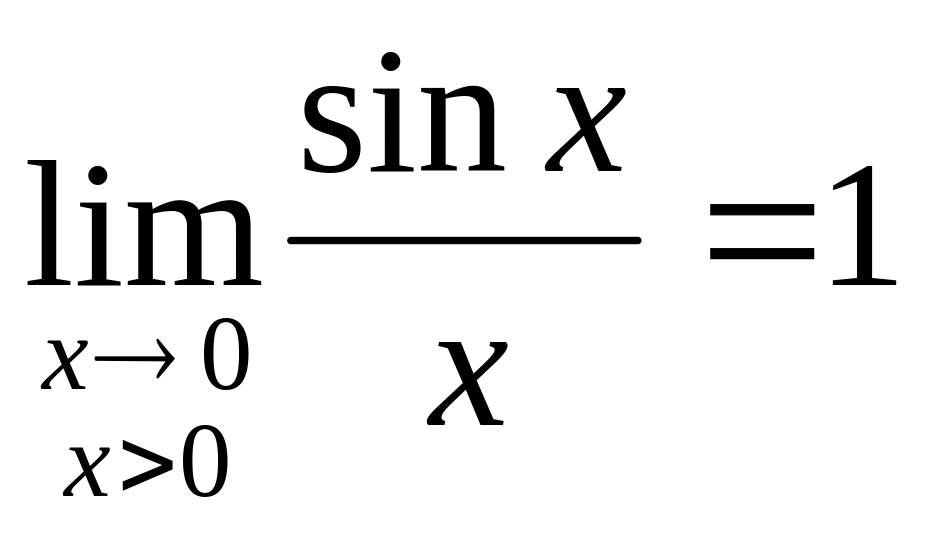А
если x<0
=>
,
где –x>0
=>
36. Второй замечательный предел.
Как
известно, предел числовой последовательности
,
имеет предел равный e.
.
1.Пусть
.
Каждое значение x
заключено между двумя положительными
целыми числами:
,
где n=[x]
– это целая часть x.
Отсюда следует
,
поэтому
.
Если
,
то
.
Поэтому:
,
.
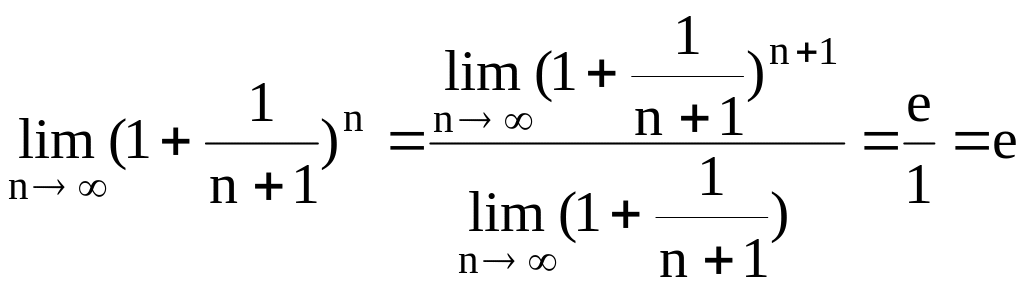По признаку существования пределов:
.
2. Пусть
.
Сделаем подстановку –x=t,
тогда
=
.
и
называются вторым замечательным
пределом. Они широко используются при
вычислении пределов. В приложениях
анализа большую роль играет показательная
функция с основанием e.
Функция
называется экспоненциональной,
употребляется также обозначение
.