1 2.2) Биномиальная формула.

Рассмотрим произведение

здесь скобок, после раскрытия которых получается сумма одночленов вида .

Выясним, сколько раз встречается многочлен при данном . Он встретится столько раз, сколькими способами можно выбрать скобок, из которых берется , т.е. . Таким образом, после приведения подобных членов получим формулу

1 3.1) Раскраска графов. Раскраской графа называется такое приписывание цветов (натуральных чисел) его вершинам, что никакие две смежные вершины не получают одинаковый цвет. Пусть G – граф, k – натуральное число. Произвольная функция вида f : VG  {1,2,…, k} называется вершинной k-раскраской, или просто k-раскраской, графа G. Если позволяет контекст, то k в этом определении опускается. Раскраска называется правильной, если f(u)  f(v) для любых смежных вершин u и v. Граф, для которого существует правильная k-раскраска, называется k-раскрашиваемым (или раскрашиваемым k цветами). В определении раскраски вместо множества {1,2,…, k} можно взять произвольное k-элементное множество. Правильную k-раскраску графа можно трактовать как окрашивание каждой его вершины в один из k цветов, при этом смежные вершины должны получать различные цвета. Поскольку функция f не обязательно сюръективна (т.е. не отображение «на»), то при k-раскраске фактически может быть использовано менее k цветов. Таким образом, правильную k-раскраску графа G можно рассматривать как разбиение V₁  V₂  …  V_l = VG, l  k, множества вершин VG на не более чем k непустых классов. Классы этого разбиения называются цветными классами.

Хроматическое число.

Наименьшее возможное число цветов в раскраске называется хроматическим числом и обозначается X(G). Если (G) = k, то граф G называется k-хроматическим. Правильная k-раскраска графа G при k = (G) называется минимальной. В качестве иллюстрации рассмотрим граф G, изображенный на рис. 7.1, где указана одна из правильных 4-раскрасок. Меньшим числом цветов этот граф раскрасить правильно нельзя, так как он содержит цикл нечетной длины C₅, для пpaвильной раскраски которого нужно не менее трех цветов. Для вершины, смежной со всеми вершинами C₅, требуется новый цвет. Итак, (G) = 4. Рассмотрим задачу составления расписаний – одну из многочисленных практических задач, сводящихся к правильной раскраске графов. Предположим, что нужно прочесть несколько лекций за кратчайшее время. Чтение каждой лекции в отдельности занимает один час, но некоторые лекции не могут читаться одновременно (например, их читает один и тот же лектор). Построим граф G, вершины которого биективно соответствуют лекциям, и две вершины смежны тогда и только тогда, когда соответствующие лекции нельзя читать одновременно. Очевидно, что любая правильная раскраска этого графа определяет допустимое расписание: лекции, соответствующие вершинам графа, составляющим цветной класс, читаются одновременно. И, обратно, любое допустимое расписание определяет правильную раскраску графа G. Оптимальные расписания соответствуют минимальным раскраскам, а число часов, необходимое для прочтения всех лекций, равно (G).

Для некоторых графов с регулярной структурой хроматические числа найти несложно: (K_n) = n, (K_n – e) = n – 1, (K_p,q) = 2, ( C_2n) = 2 и (C_2n+1) = 3. Очевидно, что граф является 1-хроматическим тогда и только тогда, когда он пустой, а 2-хроматическим – когда он двудольный и непустой. Обычно 2-хроматический граф называют бихроматическим. Поэтому теорему Кенига о двудольных графах можно сформулировать в следующем виде.

Теорема 7.1. Непустой граф является бихроматическим тогда и только тогда, когда он не содержит циклов нечетной длины. Задачи определения хроматического числа и минимальной раскраски произвольного графа являются очень сложными, эффективные алгоритмы их решения неизвестны. Рассмотрим простой алгоритм построения правильной раскраски, в ряде случаев приводящий к раскраскам, близким к минимальным.

Алгоритм последовательной раскраски.

1. Произвольной вершине v₁ графа G припишем цвет 1.

2. Если вершины v₁,v₂,…,v_i раскрашены l цветами 1,2,…,l, l  i, то новой произвольно взятой вершине v_i+1 припишем минимальный цвет, не использованный при раскраске вершин из ее окружения.

Раскраска, к которой приводит описанный алгоритм, называется последовательной. Очевидно, что это – правильная раскраска. Для некоторых классов графов (например, полных k-дольных) последовательная раскраска является минимальной. В общем случае это не так.

13.2) Далее всюду рассматриваются конечные множества X = {x₁, x₂,…, x_m} и Y = {y₁, y₂,…, y_n}. Если пишем X* (или Y*), то это значит, что элементы X* (или Y*) неразличимы.Ряд комбинаторных задач о числе перестановок, размещений, сочетаний и т.д. можно интерпретировать как задачи о числе различного вида отображений конечных множеств в конечные множества.Отображение f называется сюръективным (или отображением Х на Y ), если f (X) = Y, т.е. для любого элемента yY существует его прообраз f ^–1(y)  .

Утверждение 8.1. Число всех отображений f : X  Y равно n^m. Рассмотрим построение f как поэтапный процесс. На первом шаге выбираем f (x₁), на втором – f (x₂) и т. д. На каждом из m шагов имеется n возможностей. Таким образом, общее количество разных последовательностей выборов равно n^m. Разным последовательностям выборов соответствуют разные функции.

Функция f называется сюръективной (или, коротко, сюръекция), если каждому элементу множества прибытия может быть сопоставлен хотя бы один элемент области определения. Другими словами, функция f сюръективна, если образ множества X при отображении совпадает с множеством Y: f[X] = Y.Такое отображение называется ещё отображением на.Если условие сюръективности нарушается, то такое отображение называют отображением

Утверждение 8.5. А. Число сюръективных отображений f : X*  Y (X* означает, что элементы X неразличимы) равно 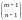; Б. Число всех отображений f : X*  Y равно . А) Так как f – сюръективное отображение, то справедливо

| f ^–1(y₁) | + | f ^–1(y₂) | + | f ^–1(y₃) | + . . . + | f ^–1(y_n) | = m ,

где | f^–1(y_i) | = a_i > 0, i = 1, 2,…, n, или a₁ + a₂ + … + a_n = m. Поставим в соответствие набору (a₁, a₂,…, a_n) двоичный вектор, в котором a_i единиц разделяются 0

(8.1) Очевидно, что соответствие между векторами (8.1) и сюръективными отображениями f является биекцией (элементы X* неразличимы). Подсчет векторов (8.1) можно трактовать как подсчет расстановок n – 1 перегородок (нулей) на m – 1 место между m единицами (две перегородки не могут располагаться рядом из-за сюръективности f ). Ясно, что это можно сделать 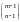способами. Б) Если f не являться сюръекцией, то прообразы некоторых элементов yY могут не существовать, т.е. | f (y) |^–1 = 0. Это значит, что в любой промежуток разрешается ставить любое количество перегородок. Подсчитаем число таких расстановок. В (8.1) имеется m – n + 1 мест для единиц и перегородок. Ставим на любые n – 1 из них перегородки, а оставшиеся места автоматически заполняются 1. Число способов сделать это равно .

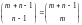14.1) Оценки хроматического числа Поскольку задачу правильной раскраски точно решить трудно, то актуальны оценки хроматического числа, выражаемые в терминах более или менее просто вычислимых параметров графа. Рассмотрим несколько оценок хроматического числа, связанных со степенями вершин графа. Обозначим через  множество всех порожденных подграфов графа G, а через (G), как обычно, – минимальную из степеней вершин графа G.

Теорема Брукса. Теорема 7.4. (Р.Брукс, 1941 г.) Если G – связный граф, не являющийся полным, и (G)  3 , то (G)  (G).Оценка, устанавливаемая теоремой Брукса, достижима (например, на графе, состоящем из цикла нечетной длины и единственной висячей вершины). Однако теорема может дать и завышенную оценку хроматического числа. Например, из этой теоремы следует, что (K_1,n)  n, в то время как (K_1,n) = 2.

14.2) Разбиение чисел на слагаемые Разбиением называется представление натурального числа в виде суммы натуральных слагаемых, а сами слагаемые — частями разбиения. Порядок слагаемых не играет роли; так разбиения 3=1+2 и 3=2+1 не различаются. Мы будем записывать разбиения, перечисляя их части через запятую в невозрастающем порядке. Например, разбиение 4=2+1+1 записывается как (2, 1, 1).

15.1.) Реберной k-раскраской графа G называется функция , ставящая в соответствие каждому его ребру e число (e) из множества {1, 2,…,k}. Минимальное число k, при котором граф G является реберно k-раскрашиваемым, называется хроматическим индексом (или хроматическим классом, реберным хроматическим числом) графа G и обозначается через ’(G). Если ’(G) = k, то граф G называется реберно k-хроматическим. Поскольку ребра любого графа G смежны тогда, когда смежны соответствующие вершины реберного графа L(G), то ’(G) можно определить как вершинное хроматическое число графа L(G), т. e. ’(G) = ( L(G)). Теорема Визинга. Для любого графа G верны неравенства (G)  ’(G)  (G) + 1. Хроматическое число графа определяется сложно: несмотря на то, что величина ’(G) может принимать только два значения — (G) и (G) + 1 — ее определение является весьма трудной задачей. Приведем значение хроматического индекса полных графов: ’(K2n+1) = (K2n +1) = 2n + 1 и ’(K2n) = (K2n) = 2n – 1.

15.2.) Рекуррентным соотношением, рекуррентным уравнением или рекуррентной формулой называется соотношение вида , которое позволяет вычислять все члены последовательности 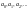, если заданы ее первые k членов. В случае, когда рекуррентное соотношение линейно и однородно, т. е. для некоторого k найдутся такие константы 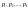, ( 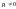), что выполняется соотношение вида 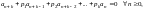то последовательность 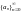называется возвратной.

Примеры. 1. Формула 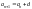задает арифметическую прогрессию. 2. Формула определяет геометрическую прогрессию.