1.1Типы графов. Пусть V — непустое множество, VV — множество всех его двухэлементных подмножеств. Пара (V, E), где E — произвольное подмножество множества VV, называется графом (неориентированным графом). Рассматриваются только конечные графы, т. е. множество V предполагается конечным. Элементы множества V называются вершинами графа, а элементы множества E — ребрами. Итак, граф — это конечное множество V вершин и множество E ребер, EVV. Множества вершин и ребер графа G обозначаются VG и EG соответственно. Вершины и ребра графа называются его элементами. Число |VG | вершин графа G называется его порядком. Если |VG | = n и |EG | = m, то G называют (n, m)-графом.

Две вершины u и v графа смежны, если множество {u, v} является ребром, и не смежны в противном случае. Если e = {u, v} — ребро, то вершины u и v называют его концами. В этой ситуации говорят также, что ребро e соединяет вершины u и v. Такое ребро обозначается символом uv. Два ребра называются смежными, если они имеют общий конец.

Вершина v и ребро e называются инцидентными, если v является концом ребра e (т. е. e = uv), и не инцидентными в противном случае. Заметим, что смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.

М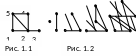 ножество всех вершин графа G, смежных с некоторой вершиной , называется окружением вершины и обозначается через N_G(v) или просто N(v).

Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. При этом точки соответствуют вершинам графа, а соединяющие пары точек линии — ребрам. В качестве иллюстрации рассмотрим граф G на рис. 1.1. Это (5, 6)-граф, VG = {1, 2, 3, 4, 5}, EG = {{1, 2}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {4, 5}}. Вершины 1 и 2 смежны, а 1 и 3 не смежны. Вершина 1 и ребро {1, 2} инцидентны, N(2) = {1, 3, 4, 5}.

Рассмотрим графы специального вида, часто используемые в дальнейшем. Граф G называется полным, если любые две его вершины смежны. Полный граф порядка n обозначается символом K_n, число ребер в нем равно, очевидно, n(n–1)/2. На рис. 1.2 изображены графы K_n для n  5. Граф называется пустым, если в нем нет ребер. Пустой граф порядка обозначается через O_n.

На рис. 1.3 показаны простые циклы C_n (n = 3, 4) и простые цепи P_n (n = 2, 3, 4). Очевидно, что K₂ = P₂ , а K₃ = C₃. На рис. 1.4 приведены два изображения простого цикла C₅ и граф Петерсена, который получается соединением двух таких циклов.

На рис. 1.5 изображены колеса W_n (n = 3, 4, 5). Заметим, что W₃ = K₄ и | W_n | = n + 1.

Г раф называется двудольным, если существует такое разбиение множества его вершин на две части (доли), что концы каждого ребра принадлежат разным частям. Если при этом любые две вершины, входящие в разные доли, смежны, то граф называется полным двудольным. Полный двудольный граф, доли которого состоят из p и из q вершин, обозначается символом K_p,q. При p = 1 получаем звезду K_1,q. Очевидно, что K_1,1 = K₂ = P₂, K_1,2 = P₃ и K_2,2 = C₄.

Н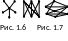 а рис. 1.6 изображены звезда K_1,5 и полный двудольный граф K_3,3. Заметим, что одна из долей двудольного графа может быть пустой. Так, O₁ — двудольный граф с одной пустой долей, O₂ можно трактовать как двудольный граф с двумя одновершинными долями или как двудольный граф, одна из долей которого содержит две вершины, а другая является пустым множеством. Аналогично двудольным определяется k-дольный и полный k-дольный графы для k > 2. На рис. 1.7 приведен трехдольный граф.

Иногда приведенное выше определение графа оказывается недостаточным и приходится рассматривать более общие объекты, в которых две вершины могут соединяться более чем одним ребром. Так возникает понятие «мультиграф». Мультиграф — это пара (V, E), где V — непустое множество вершин, а E — семейство подмножеств множества VV (ребер). Употребление термина «семейство» вместо «множество» означает, что элементы множества VV могут в E повторяться, т. е. допускаются кратные ребра.

Дальнейшее обобщение состоит в том, что кроме кратных ребер допускаются еще петли, т. е. ребра, соединяющие вершину саму с собой. Псевдограф — это пара (V, E), где V — непустое множество вершин, а E — некоторое семейство неупорядоченных пар вершин (ребер), не обязательно различных. На рис. 1.8 изображены мультиграф и псевдограф.

И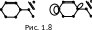 зучаются также ориентированные графы. Тогда множество VV двухэлементных подмножеств заменяется декартовым квадратом VV, состоящим из упорядоченных пар элементов множества V. Итак, ориентированный граф (или орграф) — это пара (V, A), где V — множество вершин, A — множество ориентированных ребер, которые называются дугами, A  VV. Если a = (v₁, v₂) — дуга, то вершины v₁ и v₂ называются ее началом и концом соответственно. На рисунке дуги отмечаются стрелками, указывающими направление от начала к концу (см. рис. 1.9). Аналогично определяется ориентированный мультиграф (см. рис. 1.10). Рассматриваются также смешанные графы, у которых есть и дуги, и неориентированные ребра.

Для всех этих видов графов естественно вводится понятие изоморфизма как биекции между множествами вершин, сохраняющей смежность, кратности ребер, петли и направления дуг.

Н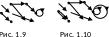 еориентированный мультиграф, получающийся в результате снятия ориентации с дуг орграфа G, называется основанием G. Ориентированный граф называется турниром, если его основание является полным графом. Этот класс графов получил свое название в связи со спортивными турнирами без ничьих, проводимых по круговой системе. Результаты встреч можно описать орграфом, вершины которого соответствуют участникам соревнования, а дуга проводится из вершины u в вершину v, если участник u победил участника v.

В лекциях будут рассматриваться графы в смысле нашего первого определения, называемые еще простыми или обыкновенными графами.

Подграфы. Операции над графами

Граф H называется подграфом (или частью) графа G, если VH  VG и EH  EG. Если H — подграф графа G, то говорят, что H содержится в G. Подграф H называется остовным подграфом, если VH = VG. Если множество вершин подграфа H есть U, а множество его ребер совпадает с множеством всех ребер графа , оба конца которых принадлежат U, то H называется подграфом,

п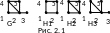 орожденным (или индуцированным) множеством U, и обозначается через G(U ).

На рис. 2.1 изображены граф G и три его подграфа H₁, H₂ и H₃, среди которых H₃ является остовным, а H₂ — порожденным.

Важный класс подграфов составляют подграфы, полученные в результате удаления вершин. Пусть v — вершина графа G. Граф G_v = G – v получается из графа G в результате удаления вершины и всех инцидентных ей ребер. Очевидно, что G_v = G (VG \ v). Подграф, множество вершин которого совпадает с множеством вершин всего графа, называется остовным подграфом.

Удаление вершины или ребра, а также переход к подграфу — это операции, с помощью которых можно из имеющегося графа получать другие графы с меньшим числом элементов. Известны также операции, позволяющие, наоборот, получать из имеющихся графов «большие» графы. Такова, например, операция добавления ребра: если вершины u и v графа G не смежны, то можно определить граф G + e, где e = uv. Он получается из графа G добавлением нового ребра e.

О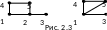 дной из наиболее важных является операция объединения. Граф H называется объединением (или наложением) графов F и G, если VH = VF  VG и EH = EF  EG (рис. 2.2). В этой ситуации пишут H = F  G. Объединение VF  VG называется дизъюнктным, если VF  VG = . Аналогично определяются объединение и дизъюнктное объединение любого множества графов, причем в последнем случае никакие два из объединяемых графов не должны иметь общих вершин.

Еще одна операция — отождествление (или слияние) вершин. Пусть u и v — две вершины графа G и H = G – u – v. К графу присоединим новую вершину v’, соединив ее ребром с каждой из вершин, входящих в объединение окружений вершин u и v в графе G. Говорят, что построенный граф получается из графа G отождествлением вершин u и v.

Стягивание ребра uv означает отождествление смежных вершин u и v. На рис. 2.3 показаны граф G и граф, полученный из стягиванием ребра .

Граф H называется стягиваемым к графу G, если H получается из G в результате некоторой последовательности стягиваний ребер. Легко видеть, например, что граф Петерсена (рис. 1.4 справа) стягиваем к K_n , n < 5. Очевидно, что любой непустой связный граф, отличный от K₁, стягиваем к K₂. Но уже не любой связный граф стягивается к графу K₃. Например, простая цепь P_n не стягивается к K₃.

1.2 Формула для числа сюръективных отображений , не включающая чисел Стирлинга. Число разбиений m-элементного множества на k непустых подмножеств обозначим через S(m, k) и будем называть его числом Стирлинга второго рода.

Утверждение 9.1 А. Число сюръективных отображений f : X  Y* (элементы Y неразличимы) равно S(m, n).

Б. Число сюръективных отображений f : X  Y равно n!S(m, n).

В. Число всех отображений f : X  Y* равно . Каждое сюръективное отображение f множества X на множество Y порождает разбиение X = f ^–1(y₁)  f ^–1(y₂)  f ^–1(y₃)  . . . f ^–1(y_n), f ^–1(y_i)   для всех i.

Если два отображения f₁ и f₂ порождают одно и то же разбиение, значит существует такая перестановка (i₁, i₂,…, i_n) чисел 1,2,…,n, что f ^–1( y_ik ) = f ^–1( y_k ), k = 1, 2,…, n. Это как раз и означает, что если элементы Y неразличимы, то f₁ и f₂ совпадают. Тем самым, пункт «А» доказан.

Любое сюръективное отображение f : X  Y можно построить в два этапа: сначала разбить X на n непустых частей X₁, X₂, …, X_n (имея в виду, что все элементы из одной части будут отображаться в один и тот же элемент множества Y ), а затем для каждого такого разбиения (X₁, X₂, …, X_n ) выбрать в качестве f (X₁), f( X₂), …, f (X_n) различные элементы Y. Согласно пункту «А» имеется S(m, n) разных исходов первого этапа. Для любого исхода первого этапа имеется n! разных исходов второго этапа. Итого имеется n!S(m, n) возможностей.

Если f не является сюръективным, то прообразы некоторых s элементов из Y не существуют, т. е. f ^–1( y_ik ) = , k = 1, 2,…, s. Это порождает разбиение множества X на n – s непустых подмножеств, где s = 1, 2,…, n – 1. Суммируя по s и добавляя количество сюръективных отображений, получим требуемое.

2.1 Степенная последовательность графа. Лемма о рукопожатиях. Критерий графичности последовательности.

Степенью вершины графа G называется число инцидентных ей ребер, т. е. число вершин в ее окружении. Будем обозначать степень вершины v через deg(v) (или deg v). Тем самым deg v = |N(v)|. Максимальная и минимальная степени вершин графа G обозначаются символами (G) и (G) соответственно: , .

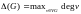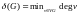Список степеней вершин графа называется его степенной последовательностью. Порядок членов в этой последовательности роли не играет. Вершина степени 0 называется изолированной, вершина степени 1 — концевой (или висячей). Ребро, инцидентное концевой вершине, также называется концевым. Рассмотрим сумму степеней всех вершин графа. Каждое ребро вносит в эту сумму 2, поэтому верно

Утверждение 2.8. («лемма о рукопожатиях»). Сумма степеней всех вершин графа — четное число, равное удвоенному числу ребер:

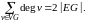Возможная интерпретация этой леммы такова: поскольку в каждом рукопожатии участвуют две руки, то при любом числе рукопожатий общее число пожатых рук четно (при этом каждая рука учитывается столько раз, во скольких рукопожатиях она участвовала).

Следствие 2.9. В любом графе число вершин нечетной степени четно.

Понятие степени вершины и лемма о рукопожатиях cохраняются для мульти- и псевдографов. При этом каждая петля вносит в степень соответствующей вершины двойку.

Граф называется регулярным (или однородным), если степени всех его вершин равны; степенью регулярного графа называется

степень его вершин. Степень регулярного графа G обозначается через deg G.

Последовательность (d₁, d₂, …, d_n) целых неотрицательных чисел ниже называется n-последовательностью и обозначается одной буквой d. Произвольная n-последовательность d называется графической, если существует граф, степенная последовательность которого совпадает с d. Этот граф называется реализацией последовательности d. Очевидно, что порядок членов в графической n-последователь-ности d несуществен, а каждый ее член d_i удовлетворяет неравенствам 0  d_i  n – 1. Часто удобно эти последовательности считать невозрастающими. Согласно лемме о рукопожатиях сумма всех членов графической последовательности является четным числом. Назовем n-последовательность d правильной, если выполняются два следующих условия: 1) n – 1  d₁  d₂  …  d_n , 2) d₁ + d₂ +… + d_n — четное число.

Без ограничения общности графическую последовательность можно всегда считать правильной.

Рассмотрим последовательность d = (2, 2, 2, 2, 1, 1, 1, 1). Существуют ровно пять графов (не обязательно связных), являющихся реализациями последовательности d. Они имеют следующие компоненты связности: 1) C₄, K₂ и K₂ ; 2) K₃ , P₃ и K₂ ; 3) P₆ и K₂ ; 4) P₅ и P₃ ; 5) P₄ и P₄..

В общем случае графическая последовательность имеет много реализаций и их число определить сложно.

Итак, графическую последовательность всегда можно считать правильной. Кроме того, в ней должны быть равные члены (если длина ее n  1), поскольку не существует графа, степени всех вершин которого попарно различны (почему

Однако указанные условия отнюдь не являются достаточными для графичности последовательности. Очевидно, например, что последовательность (3,3,1,1) не является графической, хотя и удовлетворяет упомянутым условиям. Известно несколько критериев графичности последовательности. Мы укажем один из них.

Теорема 2.10. (П. Эрдёш, Т. Галлаи, 1960 г.). Правильная n-последовательность d является графической тогда и только тогда, когда для каждого k = 1,2,…,n – 1 верно неравенство

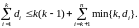
При тестировании последовательности с помощью этого критерия нет необходимости проверять все n – 1 неравенств. Установлено, что достаточно проверить k(d) = max{i : d_i  i} первых неравенств.

2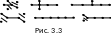 .2 Теорема о центре дерева. Цикломатическое число графа. Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется ациклическим (или лесом). Таким образом, компонентами леса являются деревья. На рис. 3.3 изображены все деревья с шестью вершинами.

Центр любого дерева состоит из одной или из двух смежных вершин.

 Доказательство проведем индукцией по числу вершин дерева. Очевидно, что концевые вершины дерева T являются центральными только для T = K₁ или T = K₂. Пусть T — дерево порядка n > 2. Удалив из T все концевые вершины, получим дерево T’, в котором по предположению индукции центр состоит из одной или из двух смежных вершин. Заметим, что для любой вершины дерева ее эксцентриситет всегда равен расстоянию до некоторой висячей вершины. Тогда эксцентриситет каждой вершины в T’ на единицу меньше ее эксцентриситета в дереве T. Следовательно, центры деревьев T и T’ совпадают.

Следствие 3.8. Число ребер произвольного (n, m)-графа G, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно m – n + k, где 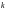— число компонент связности графа G.

Если (n₁, m₁)-граф H является одной из компонент графа G, то для превращения ее в остовное дерево нужно удалить m₁ – (n₁ – 1) подходящих ребер. Суммируя по всем k компонентам, получим требуемое. Число (G) = m – n + k называется цикломатическим числом графа G. Очевидно следствие

Следствие 3.9. а) граф является лесом тогда и только тогда, когда (G) = 0; б) граф G имеет единственный цикл тогда и только тогда, когда (G) = 1; с) граф, в котором число ребер не меньше, чем число вершин, m  n, содержит цикл.

Очевидно, что число остовов в K_n равно числу помеченных деревьев порядка n. В 1897 г. А. Кэли показал, что число помеченных деревьев порядка n равно n^n–2.

3.1 Критерий двудольности графа Известен простой критерий двудольности графа в терминах длин циклов.

Теорема 3.1. (Кёниг, 1936 г.). Для двудольности графа необходимо и достаточно, чтобы он не содержал циклов нечетной длины.

Необходимость. Пусть G — двудольный граф, C — один из его циклов длины k. Пройдем все ребра этого цикла в той последовательности, в какой они на нем расположены, начиная с некоторой вершины v. Сделав k шагов, вернемся в v. Так как концы каждого ребра лежат в разных долях, то k — четное число.

Достаточность. Не ограничивая общности, можно рассматривать только связные графы, т. к. дизъюнктное объединение двудольных графов также двудольно. Пусть связный граф G порядка n > 1 не имеет циклов нечетной длины. Построим разбиение вершин графа VG = A  B относительно вершины v  VG следующим образом: произвольную вершину u отнесем к классу A, если расстояние d(u, v) — четное число, и к классу B, если это расстояние нечетно. Покажем, что порожденные подграфы G(A) и G(B) являются пустыми. Пусть, напротив, существуют две смежные вершины u и w, входящие в один класс, т. е. d(v, u) = d(v, w). Ясно, что ни одна из них не совпадает с v, так как v  A, а смежные с ней вершины находятся B. Пусть v₁ — последняя, считая от v, общая вершина (v, u)-цепи и (v, w)-цепи (см. рис. 9.1). Так как эти цепи имеют начальные (v, v₁)-подцепи одинаковой длины, то (v₁, u)-подцепь и (v₁, w)-подцепь будут иметь одинаковую длину. Объединяя эти подцепи и ребро uw, получим цикл нечетной длины. 

Следствие 3.2. Граф является двудольным тогда и только тогда, когда он не имеет простых циклов нечетной длины.

Tеорема Кёнига подсказывает простой способ распознавания двудольности графа. Этот способ основан на простом приеме, называемом поиском в ширину. Поиск в ширину следующим образом приписывает вершинам рассматриваемого графа номера 0, 1, 2,... Начиная с произвольной вершины, приписываем ей номер 0. Каждой вершине из окружения вершины 0 приписываем номер 1. Теперь рассматриваем поочередно окружения всех вершин с номером 1 и каждой из входящих в эти окружения вершин, еще не занумерованных, приписываем номер 2. Рассматриваем окружения всех вершин с номером 2 и т. д., пока возможно. Если исходный граф G связен, то поиск в ширину занумерует все его вершины.

Далее, разобьем множество VG на две части — A и B, отнеся к A все вершины с четными номерами, а к B — все остальные вершины, и рассмотрим порожденные подграфы G(A) и G(A). Если оба они пусты (достаточно проверить, что все пары вершин с равными номерами не смежны), то G — двудольный граф с долями A и B. В противном случае граф G не является двудольным.

3.2 Число всех беспорядков на множестве {1,2,…,n} Теорема 12.3. Для чисел Стирлинга второго рода справедливо

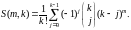Пусть S_n множество всех перестановок чисел 1, 2,…, n. Обозначим через (k) k-ый элемент перестановки . Назовем беспорядком, если 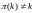при любых . Обозначим через D_n множество всех беспорядков на 1, 2,…, n.

Теорема 12.4. Число | D_n | всех беспорядков на множестве {1, 2,…, n} равно

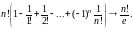Рассмотрим множества 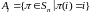, i = 1, 2,…, n. Тогда перестановка  является беспорядком тогда и только тогда, когда 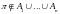. Согласно формуле включения и исключения, имеем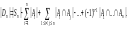

Для произвольной последовательности пересечение 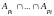есть множество таких перестановок , для которых (j) = j для 1  j  i. Поэтому 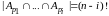. Заметив, что последовательность 1  p₁ < p₂ <…< p_i  n можно выбрать 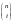способами, в итоге имеем 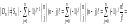

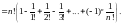
Отметим, что сумма в скобках является начальным членом следующего ряда 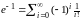, т.е. беспорядки составляют 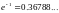всех перестановок. Например, пусть n страниц рукописи были перепутаны порывом ветра и сложены затем произвольно (вначале порядок страниц рукописи определяется их нумерацией). Из полученной формулы для D_n следует, что при больших n вероятность того, что нет ни одной страницы на правильном месте, больше чем 1/3.

Билет № 4. 1.Реберный граф и его свойства. Для произвольного графа G реберный граф L(G) определяется следующими двумя условиями: 1.вершина L(G) ставятся в соответствие ребрам G, т.е. VG(L(G))=EG; 2. вершина e1 и e2 смежны в L(G) тогда и только тогда когда ребра е1 и е2 смежны G.

Свойство: 2. Формула включений и исключений.   Комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом.

Например, в случае двух множеств   формула включений-исключений имеет вид:

В терминах множеств

Пусть   — конечные множества. Формула включений-исключений утверждает:

При   получаем формулу для двух множеств, приведенную выше.

В терминах свойств Принцип включений-исключений часто приводят в следующей альтернативной формулировке ^[4]. Пусть дано конечное множество  , состоящее из   элементов, и пусть имеется набор свойств  . Каждый элемент множества   может обладать или не обладать любым из этих свойств. Обозначим через   количество элементов, обладающих свойствами   (и, может быть, некоторыми другими). Также через   обозначим количество элементов, не обладающих ни одним из свойств  . Тогда имеет место формула:

Формулировка принципа включений-исключений в терминах множеств эквивалентна формулировке в терминах свойств. Действительно, если множества   являются подмножествами некоторого множества  , то в силу правил де Моргана   (черта над множеством — дополнение в множестве  ), и формулу включений-исключений можно переписать так:

Если теперь вместо «элемент   принадлежит множеству  » говорить «элемент   обладает свойством  », то мы получим формулировку принципа включений-исключений в терминах свойств, и наоборот.