2. Число всех беспорядков на множестве {1,2,…,n} равно

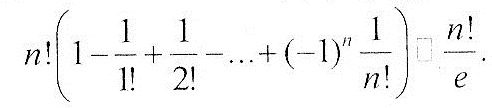
*Рассмотрим множества .Тогда перестановка П является беспорядком тогда и только тогда, когда .Согласно формуле включения и исключения, имеем

Для произвольной последовательности пересечение есть множество таких перестановок П, для которых П(j)=j для . Поэтому .Заметив, что последовательность можно выбрать способами, в итоге имеем

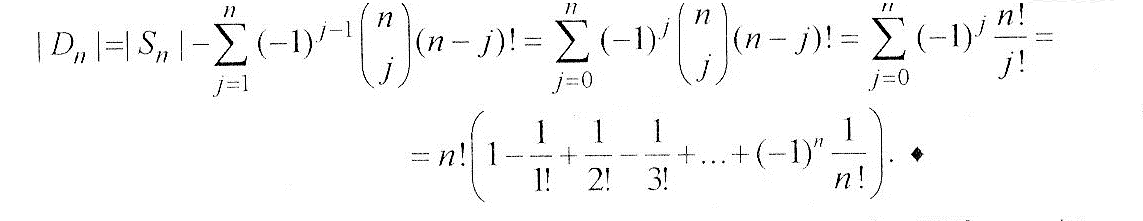
Отметим, что сумма в скобках является начальным членом следующего ряда , т.е.беспорядки составляют е^-1 =0,36788… всех перестановок. Например, пусть n страниц рукописи были перепутаны порывом ветра и сложены затем произвольно( вначале порядок страниц рукописи определяется их нумерацией). Из полученной формулы для D_n следует, что при больших n вероятность того, что нет ни одной страницы на правильном месте, больше чем1/3.

БИЛЕТ 9 Теорема Хивуда о раскраске плоских графов (Р. Хивуд, 1890 г.). Каждый планарный граф 5-раскрашиваем.

Проведем доказательство индукцией по числу вершин графа. Теорема справедлива для графов с не более чем пятью вершинами. Предположим, что она верна для графов порядка, не превосходящего n  5.

Р ассмотрим произвольный плоский граф с n + 1 вершинами. Тогда в нем найдется некоторая вершина v₀, степень которой не превосходит пяти. Действительно, если это не так, т.е. все вершины будут иметь степень более 5. Отсюда немедленно следует нарушение ограничения для количества ребер в плоском графе: m  3n – 6 (проверьте!).

Пусть N = N(v₀) – окружение вершины v₀ в графе G. Отдельно рассмотрим два случая.

1) |N|  4. По индуктивному предположению граф G – v₀ 5-раскрашиваем; раскрасим его вершины пятью цветами. Затем окрасим вершину v₀ в тот из пяти цветов, который не использован при раскраске вершин из N.

2) |N| = 5. В множестве N существуют две несмежные вершины v₁ и v₂, иначе G(N) изоморфен K₅ и граф G не планарен. Граф G’, полученный из G – v₀ слиянием этих вершин в вершину v (см. рис. 7.3), является плоским и по индуктивному предположению 5-раскрашиваемым. Фиксируем какую-либо из его правильных 5-раскрасок. В графе G окрасим вершины v₁ и v₂ в цвет вершины v, а остальные отличные от v вершины – в те же цвета, что и соответствующие вершины графа G’. Припишем вершине v₀ цвет, не использованный при раскраске вершин из N.

Биномиальная формула (бином Ньютона)

Рассмотрим произведение

здесь скобок, после раскрытия которых получается сумма одночленов вида .

Выясним, сколько раз встречается многочлен при данном . Он встретится столько раз, сколькими способами можно выбрать скобок, из которых берется , т.е. . Таким образом, после приведения подобных членов получим формулу

БИЛЕТ 10 Теорема (Критерий Понтрягина – Куратовского). Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных K₅ или K_3,3.

Тем самым можно утверждать, что многие графы непланарны и независимо от того, как они изображены на плоскости, некоторые их ребра обязательно пересекаются.

Необходимость условий теоремы уже доказана, поскольку доказана непланарность графов K₅ и K_3,3 (утверждения 5.11 и 5.12). Доказательство достаточности довольно трудоемко и поэтому опускается.

В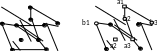 качестве иллюстрации рассмотрим граф Петерсена на рис. 5.5. Он содержит подграф, гомеоморфный графу K_3,3 (вершины из одной доли помечены одинаковой цифрой). Следовательно, этот граф не является планарным.

Формула включений и исключений

Теорема (Формула включений и исключений).

(12.3)

 Каждый x элемент из A₁…A_n дает единицу в |A₁…A_n|. Покажем, что такой же вклад x вносит в правую часть равенства (12.3). Пусть, для определенности, x входит ровно в m множеств: xA_i1... A_im. Тогда элемент x подсчитывается в правой части (12.3)

(12.4) раз. Из формулы бинома Ньютона для (a + b)ⁿ при a = 1 и b = –1 следует

Используем этот факт для преобразования выражения (12.4). Имеем

11.1) Эйлеровы графы. Теорема Эйлера. Алгоритм Флери. Начало теории графов как раздела математики связывают с так называемой задачей о кёнигсбергских мостах. Эта знаменитая в свое время задача состоит в следующем. В городе Кёнигсберга было семь мостов через реку Прегель. Спрашивалось, можно ли, выйдя из дома, вернуться обратно, пройдя в точности один раз по каждому мосту? Поставим в соответствие плану города граф G, вершины которого соответствуют разделяемым рекой участкам суши. Таким образом, задача о кёнигсбергских мостах на языке теории графов формулируется так: есть ли в мультиграфе G цикл, содержащий все ребра этого графа (все сказанное в этом пункте о графах в равной степени относится к мультиграфам).

Ц икл в графе называется эйлеровым, если он содержит все ребра графа. Связный граф, в котором есть эйлеров цикл, называется эйлеровым графом. Такой граф можно нарисовать, не отрывая карандаша от бумаги и не повторяя линий.

Например, граф, изображенный на рис. 6.1, является эйлеровым, поскольку он содержит эйлеров цикл (1, 2, 3, 4, 5, 6, 4, 2, 6, 1). В этом графе есть и другие эйлеровы циклы. Ясно, что любые два таких цикла отличаются друг от друга только порядком обхода ребер.

Теорема 6.1. (Л. Эйлер, 1736 г.). Связный граф является эйлеровым тогда и только тогда, когда степени всех его вершин четны.

 Необходимость. Пусть G — эйлеров граф. Эйлеров цикл этого графа, проходя через каждую его вершину, входит в нее по одному ребру, а выходит по другому. Это означает, что каждая вершина инцидентна четному числу ребер эйлерова цикла, а поскольку такой цикл содержит все ребра графа G, то отсюда следует четность степеней всех его вершин.

Достаточность. Предположим теперь, что степени вершин графа G четны. Начнем цепь P₁ из произвольной вершины v₁ и будем продолжать ее, насколько возможно выбирая каждый раз новое ребро. Так как степени всех вершин четны, то, попав в очередную отличную от v вершину, мы всегда будем иметь в распоряжении еще не пройденное ребро. Поэтому цепь P₁ можно продолжить путем добавления этого ребра. Таким образом, построение цепи P₁ закончится в вершине v₁, т. е. P₁ непременно будет циклом. Если окажется, что P₁ содержит все ребра графа G, то это будет требуемый эйлеров цикл. В противном случае, удалив из G все ребра цикла P₁, рассмотрим граф G₁, полученный в результате такой операции. Поскольку P₁ и G имели вершины только четных степеней, то, очевидно, и G₁ будет обладать тем же свойством. Кроме того, в силу связности графа G графы P₁ и G₁ должны иметь хотя бы одну общую вершину v₂. Теперь, начиная с вершины v₂, построим цикл P₂ в графе G₁ подобно тому, как строили цикл P₁. Обозначим через P₁‘ н P₁” части цикла P₁ от v₁ до v₂ и от v₂ до v₁ соответственно (см. рис. 6.2). Тогда получим новый цикл графа P₃ = P₁'  P₂  P₁”, который, начиная с v₁, проходит по ребрам цепи P₁‘ до v₂, затем обходит все ребра цикла P₂ и, наконец, возвращается в v₁ по ребрам цепи P₁” (рис. 6.2).

Е сли цикл P₃ не эйлеров, то проделав аналогичные построения, получим еще большой цикл и т. д. Этот процесс закончится построением эйлерова цикла. 

Будем говорить, что набор реберно непересекающихся цепей (не обязательно простых) покрывает граф G, если каждое ребро графа G входит в одну из этих цепей. Пусть связный граф G содержит k вершин нечетной степени. По лемме о рукопожатиях k четно. Рассмотрим граф G’, полученный добавлением к G новой вершины v и ребер, соединяющих v с вершинами графа G нечетной степени. Поскольку степени всех вершин графа G’ четны, то G’ содержит эйлеров цикл. Если теперь выбросить v из этого цикла, то получится k/2 цепей, содержащих все ребра графа G, т. е. покрывающих G. С другой стороны, граф, являющийся объединением r реберно непересекающихся цепей, имеет самое большее 2r вершин нечетной степени (т. к. нечетная степень может образовываться только за счет концевых вершин цепей). Поэтому меньшим числом цепей граф G покрыть нельзя. Тем самым доказано

Следствие 6.2. Если связный граф содержит ровно k вершин нечетной степени, то минимальное число покрывающих его реберно-непересекающихся цепей равно k/2.

В частности, когда k = 2, граф имеет цепь, которая соединяет вершины нечетной степени и содержит все ребра графа. Цепь, содержащую все ребра графа, называют эйлеровой.

Естественно, возникает вопрос: как найти хотя бы один эйлеров цикл в эйлеровом графе G, т. е. как занумеровать ребра графа числами 1, 2,…, |EG| с тем, чтобы номер, присвоенный ребру, указывал, каким по счету это ребро проходится в эйлеровом цикле? Оказывается, это можно сделать, если нумеровать ребра, придерживаясь следующих двух правил:

1. Начиная с произвольной вершины u, присваиваем произвольному ребру uv номер 1. Затем вычеркиваем ребро uv и переходим в вершину v.

2. Пусть w — вершина, в которую мы пришли в результате выполнения предыдущего шага, и k — номер, присвоенный некоторому ребру на этом шаге. Выбираем любое ребро, инцидентное вершине w, причем мост выбираем только в том случае, когда нет других возможностей; присваиваем выбранному ребру номер k + 1 и вычеркиваем его.

Этот процесс, называемый алгоритмом Флёри, заканчивается, когда все ребра графа вычеркнуты, т. е. занумерованы.