§3. Поверхности
3.1. Понятие поверхности
Определение. Элементарной поверхностью называется топологический (гомеоморфный) образ плоской области
Определение. Фигура в пространстве называется простой поверхностью, если окрестность каждой её точки является элементарной.
П
римеры
Элементарные
поверхности Простые поверхности
Определение. Поверхностью называется любая фигура, которую можно покрыть конечным или счетным множеством элементарных поверхностей.
Способы задания поверхностей
1) Векторное уравнение поверхности
= x
+ y
+ z
–
=
(u,
v)
2) Параметрическое задание поверхности
x = x(u, v)
y = y(u, v)
z = z(u, v)
3) z = f (x, y) – явное уравнение поверхности
4) F(x, y, z) = 0 – неявное уравнение поверхности
Пример. (x – a)2 + (y – b)2 + (z – c)2 = R2 – неявное уравнение сферы
+
+
= 1
cos2u
sin2u
cos2v
(cos2u
+ sin2u)
sin2v
x = a
+ R cos u
cos v
y = b
+ R sin u
cos v
z = c
+ R sin v
= cos u
cos v
– параметрическое
задание сферы
= sin u
cos v
= sin v
3.2. Криволинейные координаты на поверхности
Е
x
= x(u,
v)
y
= y(u,
v)
z
= z(u,
v)
=
(u0,
v)
зависит только от v,
тогда на поверхности получается гладкая
линия, которую называют v-линией
(v
– координатная линия).
Аналогично при фиксировании параметра
v
= v0
получается координатная u-линия
u.
В общем случае эти координатные линии покрывают всю поверхность.
Если известны u
и v,
то из параметрических уравнений можно
вычислить координаты точки М(x,
y,
z),
таким образом u
и v
называют криволинейными
координатами
точки М
поверхности, а u
и v
– линиями криволинейной системы
координат на поверхности.
и
– направляющие векторы касательных к
u
и v.
Пример. Параметры u и v на сфере имеют следующий смысл: u – долгота, v – полярное расстояние, отсчитываемое от северного полюса. Линии u = const и v = const представляют собой соответственно параллели и меридианы.
3.3. Касательная плоскость и нормаль к поверхности
Определение. Поверхность
называется регулярной
класса С
k
в точке
М0,
если в окрестности этой точки её можно
задать параметрическими уравнениями
x
= x(u,
v),
y = y(u, v),
z
= z(u,
v)
такими,
что они имеют непрерывные частные
производные до порядка k
включительно, причем
и
неколлинеарны.
Пусть Ф R3 – гладкая поверхность, а М0 – некоторая её точка. Говорят, что прямая касается поверхности Ф в точке М0, если она является касательной в точке М0 к некоторой кривой, лежащей в поверхности Ф и проходящей через точку М0.
Теорема. Все прямые, касающиеся поверхности Ф в точке М0, лежат в одной плоскости.
Доказательство
следует из того, что направляющий вектор
касательной является линейной комбинацией
векторов частных производных
и
.
Определение. Плоскость, в которой лежат все прямые, касающиеся поверхности Ф в точке М0, называется касательной плоскостью.
Пкас
= [М0,
,
]
Теорема. В каждой точке гладкой поверхности Ф существует и единственная касательная плоскость.
Уравнения касательной плоскости и нормали
1. Параметрическое задание
x
= x(u,
v)
(xu,
yu,
zu),
(xv,
yv,
zv)
y = y(u, v)
z = z(u, v)
Пкас:
;
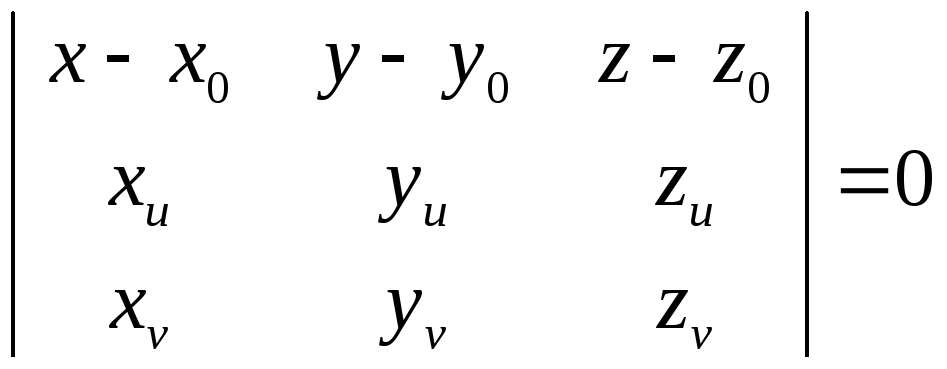n:
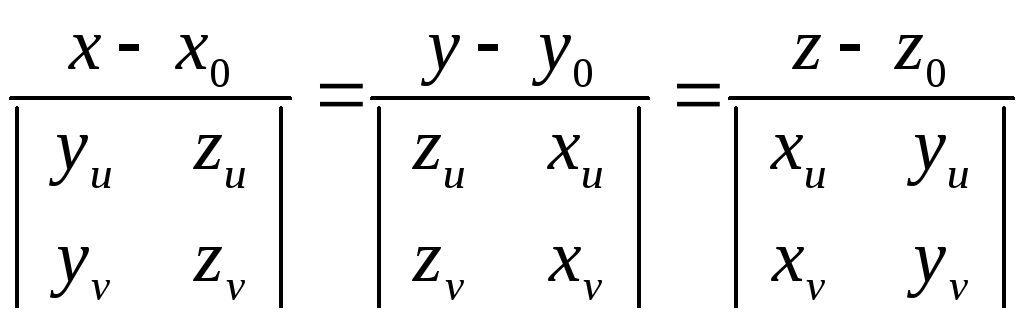
2. Явное задание Ф: z = f (x, y)
Пкас:
;
n:
3. Неявное задание поверхности Ф: F(x, y, z) = 0, М0 Ф
Пкас: F'x (x0, y0, z0) (x – x0) + F'y (x0, y0, z0) (y – y0) + F'z (x0, y0, z0) (z – z0) = 0
n:
Единичный вектор
нормали:
Пример: Написать уравнение касательной плоскости и нормали к поверхности
xy3 + z2 = 12 в точке А(1; 2; 2)
F'x = y3 = 8; F'y = 3xy2 = 12; F'z = 2z = 4
(8;
12; 4) || (2; 3; 1)
Пкас: 2(x – 1) + 3(y – 2) + (z – 2) = 0
Пкас:
2x
+ 3y
+ z
– 10 = 0 n:
