3.5.4. Гауссова и средняя кривизны поверхности

Определение. Гауссовой (полной) кривизной поверхности называется число, равное произведению главных кривизн K = k₁·k₂

Определение. Средней кривизной поверхности называется число, равное среднему арифметическому главных кривизн: H = .

Пример. В условиях предыдущей задачи найти гауссову и среднюю кривизны.

k₁ = – , k₂ = + => K = –; H =

Из уравнения главных кривизн и теоремы Виета получаем:

K = и H =

Пример. Условия те же

E = 5, F = 6; G = 10; L = ; M = 0; N =

EG – F² = 14; EN + GL – 2MF = + = , LN – M² =

K = ; H = –

Определение. Поверхности, у которых средняя кривизна во всех точках равна нулю, называются минимальными

Из всех гладких поверхностей, ограниченных данным замкнутым контуром, минимальная поверхность имеет наименьшую площадь.

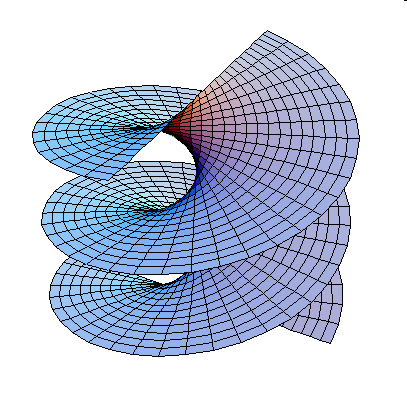
Пример. Найти гауссову и среднюю кривизны прямого геликоида (u cosv, u sinv, bv) (b > 0)

(cos v; sin v; 0) (0; 0; 0) (– sin v; cos v; 0)

(–u sin v; u cos v; b) (–u cos v; –u sin v; 0)

E = 1, F = 0; G = u² + v²; L = 0; M = – ; N = 0

EG – F² = u² + b²; LN – M² = –

EN + GL – 2MF = 0

K = – H = 0

Таким образом, прямой геликоид является минимальной поверхностью и поверхностью отрицательной кривизны.

В формуле для вычисления гауссовой кривизны знаменатель: EG – F² = || > 0, следовательно, знак гауссовой кривизны совпадает со знаком числа LN – M² => гауссова кривизна позволяет определить тип точек на поверхности.

Примеры поверхностей постоянной гауссовой кривизны

– плоскость, цилиндрические, конические (все развертывающиеся) поверхности имеют постоянную нулевую гауссову кривизну;

– сфера K = > 0 – поверхность постоянной положительной кривизны;

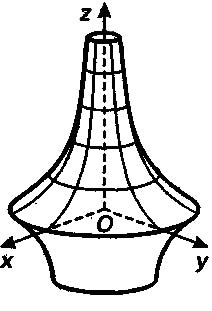
– псевдосфера (поверхность, образованная вращением трактрисы вокруг её асимптоты) – поверхность отрицательной кривизны

Трактриса Псевдосфера

x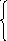 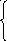= a sin t x = a sin u cos v

y = 0 y = a sin u sin v

z = a(ln tg + cos t) z = a (ln tg + cos u)

K = –

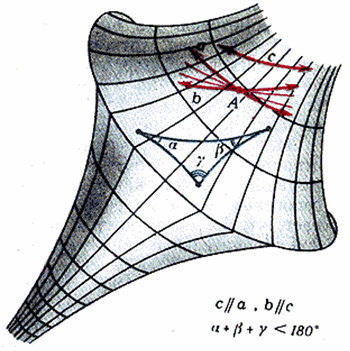
§ 4. Внутренняя геометрия поверхностей

4.1. Изометричные поверхности

Определение. Две поверхности S и S' называются изометричными, если между точками этих поверхностей можно установить такое биективное соответствие, при котором длины соответствующих кривых на поверхностях S и S' равны.

Обозначение: S S'

Если две поверхности изометричны, то говорят, что каждая из них получена изгибанием другой. Таким образом, изгибание поверхности – это такая деформация, при которой не изменяются длины кривых на поверхности.

Примеры.

1. Изгибание плоскости в двугранный угол или параболический цилиндр

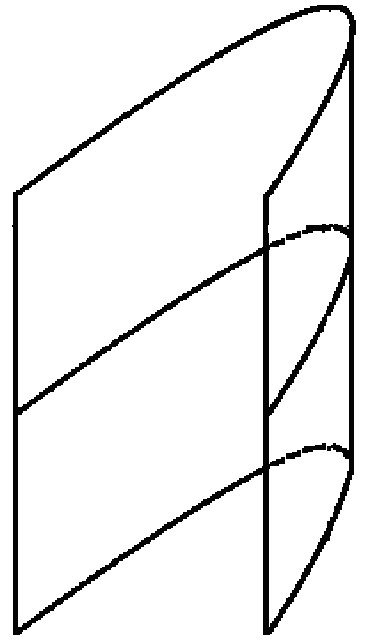
2. Изгибание многогранного выпуклого угла (например, трехгранного) в коническую поверхность, которая имеет такую же развертку и плоский угол, что и данный многогранный угол

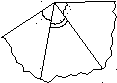
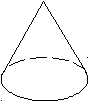
3. Если от сферы отсечь плоскостью сферический сегмент и отразить его зеркально относительно плоскости края, получим поверхность, изометричную сфере.

Теорема (признак изометричности поверхностей). Две регулярные поверхности S₁ и S₂, заданные на одной и той же области Q вектор-функциями (u, v) и (u, v) соответственно, изометричны тогда и только тогда, когда одинаковы коэффициенты первых квадратичных форм этих поверхностей

Доказательство

<=) Очевидно, так как длина дуги кривой зависит только от I.

=>) Пусть S₁ S₂ => существует изометрия f : S₁  S₂ и длины соответствующих дуг равны => I₁ = I₂ <=> dS₁² = dS₂²

Пусть ₁ – u₁-линия, ₂ – u₂-линия, ₁ ₂ =>

E₁du² + 2F₁du dv + G₁dv² = E₂du² + 2F₂du dv + G₂dv²

<=> E₁ = E₂, F₁ = F₂, G₁ = G₂