23.Закон Ампера

_Ампер эксп-но установил, что сила d(в-р)F действ на элемент тока Id(в-р)l с индукцией (в-р) B равна: 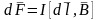– закон Ампера (сила Ампера). Если проводник прямолинейный и магнитное поле однородное (одинаковое в каждой точке), интегрируя последнее выражение, получаем: 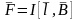. Направление силы Ампера (в-р)F опр по правилу в-рного произведения. Сила (в-р)F ┴-а пл-сти, в кот лежат в-ры l и B и напр силы (в-р)F опред правилом правого винта: «если рукоятка правого винта вращается от первого вектора l ко второму ве-ру B на кратчайший угол, то поступательное движ винта указ направление силы (в-р)F». Модуль силы Ампера:

Рассмотрим работу перемещения проводника с током в магнитном поле: На проводник с током будет действовать сила Ампера и проводник передвинется:

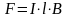
Элементарная работа при перемещении проводника:

_,

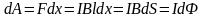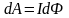
_{Конечная работа это: ,}

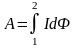24.Теорема о циркуляции

Теорема о циркуляции вектора магнитной индукции в вакууме (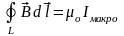 ) допускает обобщение на магнитное поле в веществе в виде: 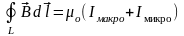, где I_макро и I_микро – алгебраическая сумма макро и микро токов через поверхность S ограниченных контуром L. Покажем теперь, что I_микро связан с намагниченностью j:

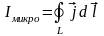
Т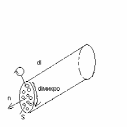 .е. сумма микро токов через поверхность S ограниченных контуром L равна циркуляции вектора намагниченности j. Рассмотрим прямой круговой намагниченный цилиндр длинной dl и площадью поперечного сечения S. Молекулярные токи внутри цилиндра текут в противоположные стороны и поэтому взаимноскомпенсированы. Нескомпенсированы только те токи, которые выходят на поверхность цилиндра и ни складываются в поверхностный ток

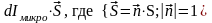
С другой стороны полный магнитный момент цилиндра по опр намагниченности равен: _,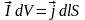

_{Так как} и 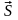направлены в одну сторону, то dI_микро=jdl. Вклад в циркуляцию намагниченность дадут только те токи, которые нанизаны как бусы на нитку. Тогда окончательно можно написать:

С учетом последнего соотношения теорема о циркуляции вектора магнитной индукции принимает вид: _,

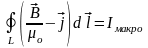
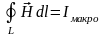_, - теорема о циркуляции магнитного поля

Циркуляция вектора напряженности магнитного поля вдоль произвольного замкнутого конура равна результирующему макро току через поверхность ограниченного этим контуром. Для изотропных магнетиков связь намагниченности j и напряженности Н магнитного поля. Т.е. 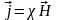χ—безразмерная величина – магнитная восприимчивость среды или вещества. Подставим в выражении для : _, ,

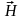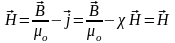Закон полного тока(теорема о циркуляции вектора магнитной индукции):циркуляция вдоль замкнутого контура вектора магнитной индукции в вакууме равна произведению магнитной постоянной ₀ на алгебраическую сумму токов охватываемых этим контуром: . Выбор направления обхода контур L согласовывается с направлением тока по правилу правого винта. Ток берётся с «+»если с острия тока I обход контура совершается против часовой стрелки иначе «-». Если замкнутый контур не охватывает проводник с током, то циркуляция вектора равна В=0. Рассмотрим доказательство для магнитного поля бесконечного прямолинейного проводника с током I в вакууме. За контур L возьмем линии индукции В находящихся на r от оси проводника с током.

I

r

B

,

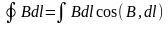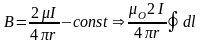
Теорема о циркуляции вектора магнитной индукции есть следствие з-на БСЛ, но она допуск обобщение на поля и люб среды. При таком обобщении эта теорема – одно из обобщ электродинамики Максвелла: 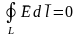. Т о цирк в-ра магн инд позвол магн поля различных конструкций токов.