21.Магнитное поле

Магнитное поле, как и эл-кое, изображается магнитными силовыми линиями – линиями (в-р) B. Линии магнитной индукции (в-р) B – это линии, касат к кот в каждой точке совпадают с напр в-ра B. Линии (в-р) B всегда замкнуты, что указывает на вихревой характер магнитного поля, на отсутствие магнитных зарядов, на кот могли бы начинаться и заканчиваться силовые линии. По густоте силовых линий судят о величине магнитного поля; там где силовые линии редкие – магнитное поле слабое.

Линии индукции прямолинейного проводника с током представляют собой концентрические окружности, центры которых лежат на оси тока.

При поступательном движении правого винта направление вращения рукоятки винта указывает направление силовых линий.

1. Электронный орбитальный магнитный момент – из-за вращения эл-нов вокруг ядер.

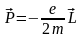
2. Электронный спиновой магнитный момент.

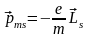, где L_s – спиновой механический момент

Если известна Е , то сила со стороны поля действующая на зар. q =:

Сила F, действующая на пробный зар. q в данной точке поля, = векторной сумме сил каждого зар. в отдельности, т.е.: , помножим на

… т.е. - принцип суперпозиции .

Напряженность Эл.п. системы зар. = векторной сумме напряженностей полей, создаваемых каждым зар. в отдельности.

Если непрерывно распределенный зар. т.е. : . Эл.п. графически изображается с помощью линий напряженности Е, силовых линий, линий Е, метод предложил Фарадей.

22.Закон Био-Савара-Лапласа

Взаимодействие между покоящимися зар. осуществляется посредством Эл.п. (электро-статического поля) . понятие Эл.п. ввел Фарадей. Неподвижный Эл.зар. изменяет свойство пространства и создает Эл.п. Оно проявляется по действию на пробный зар. Отношение силы действующей со стороны поля на пробный зар. не зависит от величины этого зар. и может хар-ть само Эл.п. , тогда приходим к характеристике поля – напряженности :

Эл.п. эсть векторная силовая характеристика поля = отношению силы, действующей на зар. со стороны поля,к зар. , т.е.: , q≷0, Напряженность поля численно = силе, действующей на единичный «+» зар. , когда q=+1. Единицы измерения напряжения , . Найдем напряжение поля точечного зар. q , находящейся в точке. Хар. вектором в среде, по З.Кулона можем записать

, - созд. точечный зар.

Если известна Е , то сила со стороны поля действующая на зар. q =:

Сила F, действующая на пробный зар. q в данной точке поля, = векторной сумме сил каждого зар. в отдельности, т.е.: , помножим на

… т.е. - принцип суперпозиции .

Напряженность Эл.п. системы зар. = векторной сумме напряженностей полей, создаваемых каждым зар. в отдельности.

Если непрерывно распределенный зар. т.е. : . Эл.п. графически изображается с помощью линий напряженности Е, силовых линий, линий Е, метод предложил Фарадей. Линии напряженности это кривые, касательный к которым в каждой точке совпадают с направлением вектора напряженности в данной точке. Линии напряженности начинаются на «+» зар. и заканчиваются на «-» или уходят в . Густота силовых линий ,т.е. число линий на ед. площади поверхности перпендикулярной к линиям. Она выбирается так, что количество линий пронизывающих ед. площади поверхности равно или пропорционально . 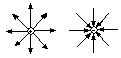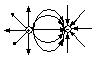По силовым линиям можно судить о величине и направлении вектора в разных точках пространства. Рассмотрим примеры силовых линий: