32. Токи при замыкании и размыка индуктивностьнии цепи содержащие

При любом изменении силы тока в проводящем контуре возникает э.д.с. самоиндукции, после чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, по правилу Ленца, всегда имеют такое направление, чтобы оказывать сопротивление изменениям тока в цепи, т. е. имеет направление, противоположное току, создаваемому источником. При выключении источника тока экстратоки так же направлены, как и ослабевающий ток. Значит, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.

Исследуем процесс выключения тока в цепи, содержащей источник тока с э.д.с. ξ , катушку индуктивностью L и резистор сопротивлением R . Под действием внешней э. д. с. в цепи течет постоянный ток

пренебрегаем внутренним сопротивлением источника тока).

В момент времени t=0 отключим источник тока. Ток в катушке индуктивностью L начнет убывать, что приведет к возникновению э.д.с. самоиндукции ξs = -L(dI/dt) оказывающей препятствие, согласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи задается законом Ома I= ξs/R, или

Разделив в формуле (1) переменные, получим (dI/I) = -(R/L)dt . Интегрируя эту формулу по I (от I0 до I) и t (от 0 до t), найдем ln (I/I0) = –Rt/L, или

где τ = L/R — постоянная, которая называется временем релаксации. Из (2) видно, что τ есть время, в течение которого сила тока уменьшается в е раз.

Значит, в процессе отключения источника тока сила тока уменьшается по экспоненциальному закону (2) и задается кривой 1 на рис. 1. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше τ и, значит, тем медленнее убывает ток в цепи при ее размыкании.

При замыкании цепи помимо внешней э. д. с. ξ возникает э. д. с. самоиндукции ξs = -L(dI/dt) оказывающая препятствие, согласно правилу Ленца, возрастанию тока. По закону Ома, IR = ξ+ξs или

Э.д.с. самоиндукции

т. е. при значительном возрастании сопротивления цепи (R/R0>>1), которая обладает большой индуктивностью, э.д.с. самоиндукции может во много раз быть больше э.д.с. источника тока, включенного в цепь. Значит, необходимо учитывать, что контур, который содержит индуктивность, нельзя резко размыкать, так как при этом (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и поломке измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции больших значений не достигнет.

33.Энергия магнитного поля

Магнитная энергия тока. Плотность магнитной энергии.

Р ассмотрим контур с индуктивностью L и током в нем I. Тогда с этим контуром сцеплен магнитный поток Ф= I L.При изменении тока на dI будет изменяться магнитный поток на величину dФ=LdI (L=const).

Д ля изменения магнитного потока на величину dФ необходимо совершить работу dA = IdФ_i dA =I LdI . Пусть ток меняется в контуре от 0 до I. Работа по созданию магнитного потока dФ через поверхность, ограниченную контуром

. Выражение называется собственной энергией тока I в контуре с индуктивностью L. Т.к. токи порождают магнитные поля, то собственная энергия тока в контуре есть энергия магнитного поля этого контура. Тогда _. Получим теперь энергию магнитного поля через характеристики магнитного поля, т.е. через и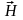 . Получим выражение W_м на примере соленоида. Индуктивность соленоида: L=μ₀μn²V. Индукция магнитного поля в соленоиде: B=μ₀μnI I=B/μ₀μn. - характеристика магнитного поля, т.к. B=μ₀μН, то

Обычно вводится пл-сть энергии магнитного поля – количество энергии в единице объема.

( B=μ₀μН),

плотность энергии электромагнитного поля складывается из энергии электрического поля и магнитного поля. . Плотность энергии электромагнитного поля:

_, т.к. ,то

L_{соленоида}=μ₀μn²V , откуда Гн/м ;