2.2 Реконструкция динамической системы методом задержки

Основная структура хаотической системы, содержащая в себе всю информацию о системе, а именно, ее аттрактор, может быть восстановлена через измерение только одной наблюдаемой этой динамической системы, фиксированной как временной ряд.

Детерминированные динамические системы описывают эволюцию системы с течением времени в некотором фазовом пространстве

Эти системы могут быть порождены, обыкновенными дифференциальными уравнениями

или, если время дискретно t = nΔt, выражениями вида

Временные ряды затем можно рассматривать как последовательность наблюдений { S_n = S(x_n) }, сделанных с помощью некоторой функции измерения s(.) . Так как последовательность (обычно скалярная) { S_n } сама по себе не порождает многомерное фазовое пространство динамической системы, необходимо использовать некоторый технический прием, чтобы раскрыть многомерную структуру, используя только имеющиеся данные.

Согласно методу Грасбергера и Прокаччи, процедура реконструкции фазового пространства и восстановления хаотического аттрактора системы при динамическом анализе временного ряда, сводится к построению так называемого лагового или восстановленного пространства с помощью метода задержки. Векторы в новом пространстве, пространстве вложения, сформированы из значений временного ряда скалярных измерений с временным запаздыванием:

Число элементов m называется размерностью вложения, время τ лагом.

В теореме Такенса показывается, что если последовательность { S_n } на самом деле состоит из скалярных измерений структуры динамической системы, тогда, при определенных предположениях, такое восстановление фазового портрета является точной картиной настоящего множества { x }, если, конечно, m достаточно велико.

Или, другими словами, реальный аттрактор динамической системы и «аттрактор», восстановленный в лаговом пространстве по временному ряду согласно указанному выше правилу (псевдоаттрактор), при адекватном подборе размерности вложения m, являются топологически эквивалентными и обладают одинаковыми обобщенными фрактальными размерностями, ляпуновскими показателями и другими численными характеристиками.

2.3 Реконструкция динамической системы с помощью отображений.

Для реконструкции динамической системы создадим n-мерное дискретное отображение

, (2.3.1)

где - координаты вектора состояния, рассмотренного в моменты времени , - нелинейные функции.

В рамках алгоритма глобальной реконструкции для получения конкретного вида эволюционного оператора функции , представляют в виде разложения по некоторому базису, ограничиваясь при этом конечным числом членов разложения. В простейшем случае задание может осуществляться полиномами некоторой степени :

, (2.3.2)

где - неизвестные коэффициенты, которые требуется найти. Для аппроксимации могут применяться полиномы Лежандра либо может использоваться более сложная методика.

Система уравнений (1.10.1) допускает запись для любого номера i. Для нахождения коэффициентов (1.10.2) необходимо решить систему N нелинейных алгебраических уравнений

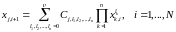, (2.3.3)

с неизвестными , в которой N – число точек скалярного временного ряда, используемых для аппроксимации правых частей, - степень полинома.

При заданных n и число коэффициентов K полиномов (1.10.2) в общем случае может быть определено по формуле . Как правило, , поэтому для конкретизации эволюционного оператора система (1.10.3) решается методом наименьших квадратов. Получающаяся математическая модель является громоздкой, но при условии удачного выбора общего вида нелинейных функций её решение воспроизводит сигнал с высокой степенью точности.