1.1.4 Корреляционная размерность

Преобразуем траекторию динамической системы на странном аттракторе в последовательность точек , а мерное фазовое пространство разделим на ячейки . Вероятность попадания точки, принадлежащей аттрактору, в ю ячейку ( ):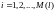

, (1.1.4.1)

где – число точек в этой ячейке.

Для описания неоднородной статистической структуры аттрактора вводится бесконечное множество размерностей 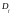, связанных с 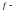ми степенями :

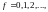; _(1.1.4.2)

Численное определение размерностей путем покрытия фазового пространства множеством кубов объема и подсчета числа точек, попадающих в выбранную ячейку, чрезвычайно трудоемко и практически невозможно для аттракторов больших размерностей. Однако для частного случая корреляционную размерность

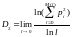_(1.1.4.3)

можно определить из корреляционного интеграла

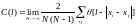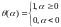, где , _(1.1.4.4)

который в свою очередь может быть оценен непосредственно для последовательности точек.

Справедливость приведенного степенного закона ограничена значениями , достаточно малыми по сравнению с размерностью аттрактора. При увеличении величина достигает насыщения (при сравнимых с размерностью аттрактора). С другой стороны, при очень малых значениях число пар точек, расстояние межу которыми не превышает , становится малым (из-за конечного числа точек) и статистика становится бедной. На практике степенной закон выполняется только в ограниченном диапазоне значений (скейлинговом диапазоне), который и может быть использован для определения корреляционной размерности.

Учитываю, что из степенного закона следует

_(1.1.4.5)

получаем оценку размерности аттрактора как тангенс угла наклона прямой, аппроксимирующей график корреляционного интеграла в двойном логарифмическом масштабе.

Корреляционный интеграл будет вычисляем на сетке расстояний . Находим скейлинговый диапазон. В данном диапазоне на сетке расстояний вычисляем корреляционную размерность по формуле:

. _(1.1.4.6)

Окончательный результат получаем путем осреднения значений, полученных на сетке расстояний из скейлингового диапазона.

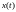При малых шагах по времени точки и 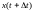будут слишком близкими, поэтому большое значение приобретает правильный выбор временной задержки . Необходимо стремиться выбрать так, чтобы корреляция между и была по возможности минимальной. Традиционный способ выбора временной задержки состоит в вычислении автокорреляционной функции временного ряда. Задержка выбирается равной времени первого пересечения нуля автокорреляционной функцией, которая может вычислена следующим образом:

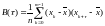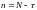, . _(1.1.4.7)

Корреляционная размерность является нижней границей размерности Хаусдорфа .

Расчет любой из фрактальных размерностей аттрактора по временному позволяет оценить (обычно снизу) минимальное число существенных динамических переменных, необходимых для описания наблюдаемых процессов. Численные методы следуют сформулированному определению. Алгоритм получается следующий. Предполагается, что по временному ряду построена -мерная реконструкция и имеется набор векторов .

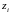1. Задаем некоторое , разбиваем область фазового пространства, в которой лежат анализируемые вектора, на кубики со стороной и подсчитываем, сколько кубиков накрывают все известные нам точки. Получаем одно значение .

Здесь необходимо обратить внимание на то, что полное количество кубиков в большом -мерном кубе, содержащем аттрактор, огромным, но подавляющее большинство из них нам не нужно, потому что туда не попадет

ни одной точки . В любом случае не может быть больше числа векторов, т.е. всегда 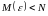. На самом деле число нужных кубиков еще меньше и можно построить быстрые и эффективные алгоритмы для расчета . Поделим все координаты векторов на и оставим только целую часть, преобразовав вектора в новые вектора . Тогда для всех векторов , попадающих в одну ячейку, полученные вектора будут совпадать. То есть просто будет равно количеству различных векторов .

2. Допустим, что мы вычислили для различных . Теперь по полученным данным необходимо оценить размерность. Как следует из определения емкости, при малых должно вести себя как , а в таком случае . Поэтому оценивание емкости по полученным данным сводится к:

1. поиску «наиболее линейного» участка зависимости

от ;

2. построению на этом участке линейной аппроксимации вида

, например, по методу наименьших квадратов; в качестве оценки емкости берется .

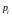Сумму , где – мера 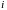–го кубика покрывающего аттрактор, называемую иногда обобщенным корреляционным интегралом, можно представить в виде

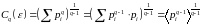, _(1.1.4.8)

т. е. как среднее (в общем случае среднее геометрическое) значение меры

кубика размера . Идея заключалась в том, чтобы оценить это среднее

как можно точнее, а для этого рассчитать меру кубика или шара радиуса

с центром в каждой точке , а затем усреднить полученные значения

по всем таким шарам. Будем обозначать через число точек внутри

-шара с центром в точке . Тогда его меру можно приближенно оценить как , а

_(1.1.4.9)

В случае это соотношение существенно упрощается, a называют корреляционным интегралом. Последняя сумма — это просто удвоенное число пар точек, расстояние между которыми не превосходит . Оказалось, что для того, чтобы оценить размерность по корреляционному интегралу, необходимы выборки существенно меньшей длины, чем в предыдущем случае. Методика оценки та же самая — линейная аппроксимация зависимости по «наиболее линейному» участку. Саму размерность называют корреляционной размерностью или корреляционным показателем.

1.1.5 Показатель Херста Показатель Херста находиться поиском угла наклона логарифмической зависимости методом (МНК)

. Зависимость меры корреляции и показателя Херста (1.1.5.1)

Существует три различных классификации для показателя Херста:

1. 

2. 

3. 

H, равное 0.5 указывает на случайный ряд. События случайны и некоррелированные. Правая часть уравнения зависимости обращается в ноль. Настоящее не влияет на будущее.

В случае . Данный диапазон соответствует антипесистентным, или эргодическим рядам. Такой тип системы называют “возврат к среднему”. Если система демонстрирует рост в предыдущий период, то скорее всего в следующем периоде начнется спад, и на оборот. Устойчивость такого антиперсистентного поведения зависит от того, на сколько H близко к нулю. Чем ближе его значение к нулю, тем ближе C к -0.5, или отрецательной корреляции. Такой ряд более изменчив или волатилен, чем ряд случайный, так как состоит из частых реверсов спад-подъем. До сих пор было найдено мало антиперсистентных рядов.

При 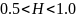– трендоустойчивые ряды. Если ряд возрастает (или убывает) в предыдущий период, то вероятно, что он будет сохранять эту тенденцию какое-то время в будущем. Трендоустойчивость поведения, или сила персистентности, увеличивается при приближении H к еденице.

1.1.6 Индекс фрактальности Пусть на отрезке [a,b] задана функция , имеющая не более конечного числа точек разрыва первого рода: именно такие функции естественно рассматривать в качестве модельных, например для финансовых временных рядов. Введем равномерное разбиение отрезка

, (1.1.6.1)

_где ( ). Покроем график этой функции прямоугольниками таким образом, чтобы это покрытие было минимальным по площади в классе покрытий прямоугольниками с основанием

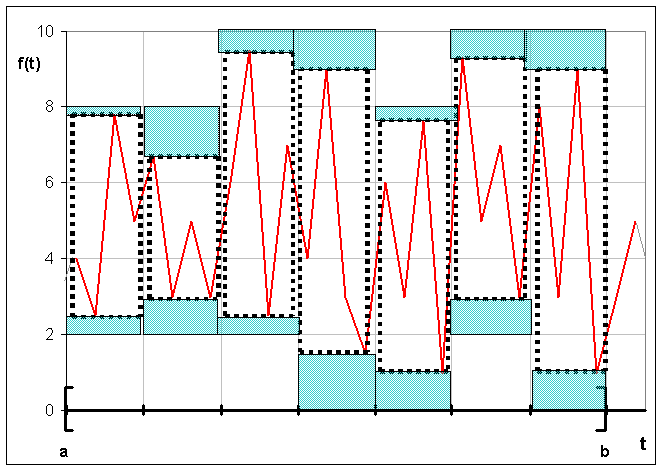
Рис.1.1 Разбиение временного ряда на прямоугольни

Тогда высота прямоугольника на отрезке будет равна амплитуде , которая является разностью между максимальным и минимальным значением функции на этом отрезке.

Введем величину:

(1.1.6.2)

Тогда полную площадь минимального покрытия можно записать в виде:

(1.1.6.2)

Поэтому из (4) следует, что

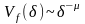при , (1.1.6.3)

где

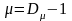(1.1.6.4)

Назовем размерность размерностью минимального покрытия. Чтобы соотнести с другими размерностями и в частности с клеточной размерностью , построим клеточное разбиение плоскости графика функции как показано на рис. 3. Пусть 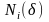- число клеток, покрывающих график внутри отрезка . Тогда из рисунка видно, что

(1.1.6.5)

Разделим это соотношение на и просуммируем по i с учетом (1.1.6.2). В результате получим

, (1.1.6.6)

где 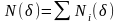есть полное число клеток размера , покрывающих график функции на отрезке [a,b]. Переходя к пределу при , с учетом (1.1.6.3) и (1.1.6.4), получим:

(1.1.6.7)

(1.1.6.8)

Следовательно .

Заметим, однако, что несмотря на это равенство, для реальных фрактальных функций минимальные и клеточные покрытия могут давать различные приближения величины к асимптотическому режиму, причем величина этого различия может быть весьма значительной.

Возвращаясь к формуле (1.1.6.4) заметим, что поскольку и для одномерной функции 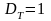, то . Поэтому в данном случае индекс 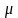естественно назвать индексом фрактальности. Далее при анализе финансовых временных рядов мы будем рассматривать его как основной фрактальный показатель.

1.2 R\S анализ

Пусть имеется последовательность 

 

котировок некоторой ценной бумаги (в общем случае — временной ряд). Образуем из данного ряда последовательность 

, где

   

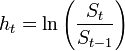
— логарифмическая доходность в момент времени t.

Для каждого натурального n составим величины

   

и вычислим следующие числовые характеристики получившейся подпоследовательности.

Пусть 

 

— среднее арифметическое элементов подпоследовательности 

Для нахождения нормированного размаха накопленных сумм посщитаем:

1. Размах накопленных сумм

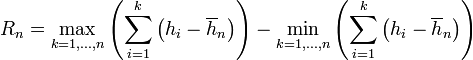  (1.2.1)

2. Среднеквадратическое отклонение

  (1.2.2)

3. Нормированный размах накопленных сумм

  (1.2.3)

Вычисляя в соответствии с вышеприведённым алгоритмом значения RS_n, образуем из них и соответствующих значений количества элементов n последовательность точек на плоскости

  .

По полученной зависимости в логарифмическом масштабе методом наименьших квадратов посчитаем угловой коэффициент прямой, проходящей максимально близко к полученным точкам.

По известной МНК-формуле, полагая

   

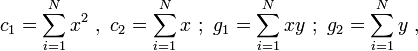
Находим коэффициент Херста

1.3 Локальный фрактальный анализ Локальный фрактальный анализ основан на последовательном вычислении в каждый момент времени индекса фрактальности, на основании некоторого количества предыдущих значений (n) временного ряда. Полученные значения в i-ый момент времени будут характеризовать состояние временного ряда на промежутке