1.6 Показатель Ляпунова

Для СДУ вида линеаризованная система имеет вид , где

_(1.6.1)

Тогда ляпуновский характеристический показатель – вещественное число, отличное от , определяется как верхний предел

(1.6.2)

Для любого решения существует ляпуновский характеристический показатель;

При умножения решения на константу ляпуновский показатель не меняется, т.е. ;

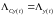Ляпуновский показатель линейной комбинации двух решений, и , меньше равен большему из показателей этих двух решений, т.е.

;

Имеется (по размерности фазового пространства) линейно независимых решений уравнения (фундаментальная система решений), которым отвечают ляпуновских показателей, нумеруемых в порядке убывания: . Наибольшее из этих чисел называют старшим ляпуновским показателем.

Определить тип регулярного аттрактора, к которому принадлежит исследуемая траектория системы, позволяют в некоторой степени показатели Ляпунова системы первого приближения, линеаризованной на этой траектории. Если все показатели Ляпунова отрицательны, то траектория – аттрактор, являющийся устойчивой особой точкой (узел или фокус). Если один (старший) показатель равен нулю, а все остальные показатели отрицательны, то траектория, скорее всего, является устойчивым циклом. Если показателей Ляпунова равны нулю, а все остальные показателей отрицательны, то траектория, скорее всего, лежит на инвариантном устойчивом - мерном торе.

Хаотическим аттрактором называется аттрактор, динамика которого характеризуется положительным показателем Ляпунова.

Рассмотрим метод Вольца расчета старшего показателя Ляпунова по реконструированным векторам . Сначала произвольная точка траектории (в реконструированном фазовом пространстве) принимается за начальную и ищется ближайшая к ней точка . Расстояние между этими двумя точками .

Рис.1.2 Схема вычисления показателя Ляпунова

При хаотической динамике со временем это расстояние растет. Если

следующее значение ,то оно отбрасывается и ищется новая точка , соседствующая с и лежащая по возможности в том же направлении, что и . Так как описывает поведение малого возмущения, его длина должна быть по возможности малой, чтобы линеаризованная вдоль траектории система хорошо описывала эволюцию. С другой стороны она не должна быть настолько малой, чтобы стать сравнимой с уровнем шумов. Кроме того, необходимо чтобы и принадлежали разным траекториям, иначе не будут получены положительные первые показатели Ляпунова . Если эти условия выполняются, то старший показатель Ляпунова определяется из выражения:

, где - число смен соседних траекторий.

2 Реконструкции динамических систем по временным рядам

2.1 Теорема Такенса

Идеи авторегрессионного анализа использовались давно, но, по-видимому, связь авторегрессиионных моделей с динамическими системами, описывающими исследуемые процессы, всерьез не анализировалась. Однако такой вопрос возник, когда в конце 70-х годов голландский математик Ф. Такенс доложил о своей теореме, которая лежит в основе всех алгоритмов анализа временных рядов методами нелинейной динамики.

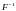Когда многообразие реализуется в виде поверхности в n-мерном пространстве, которая не пересекается сама с собой, то говорят, что оно вложено в . Само вложение можно представить как дифференцируемую векторную функцию F, определённую на , для которой отображение является взаимно однозначным и существует обратная дифференцируемая функция , отображающая в . То есть и . Заметим, что определена только на , в противном случае она не могла бы быть однозначной. Выбирая разные F и n, можно получить различные представления одного и того же многообразия. Если все F и дифференцируемы, то про эти представления говорят, что они диффеоморфны друг другу.

Лемма 1. Если M и N являются многообразиями с размерностью m и n соответственно, m <n, и является функцией множества C¹, тогда N - f(M) плотно в N.

Пусть - как минимум дважды дифференцируемое многообразие, а g(x) – некоторая дважды дифференцируемая функция, отображающая , для которой матрица производных имеет ранг k. Последнее условие необходимо, чтобы при отображении не получился объект меньшей размерности; скажем, плоскость не отображалась в одномерную кривую. Такое отображение будет давать погружение многообразия в при условии, что (теорема Уитни). Погружение локально аналогично вложению, но может содержать самопересечения, а потому глобально невозможно определить обратное отображение. Например, если в качестве многообразия рассматривать окружность, то на плоскости эллипс будет вложением, а восьмёрка – только погружением.

Лемма 2. Пусть M и N являются многообразиями с размерностью m и n соответственно, m <n, и является функцией множества C¹. Пусть . Если f погружено на каждом p, так что f(p) = q, тогда множество является подмногообразием M, чья размерность m-n.

Пусть задана динамическая система с фазовым пространством P. Будем считать, что числа образующие временной ряд, являются значениями некоторой «наблюдаемой» - скалярной функции состояния динамической системы x(t):

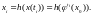
В качестве многообразия M может использоваться либо само фазовое пространство P, либо какое-либо инвариантное многообразие из P.

Рассмотрим построение вектора Пусть временной шаг между элементами временного ряда равен , а вектора будем для краткости обозначать . Тогда очевидно, что

Поэтому

Мы связали все компоненты вектора 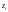с одним и тем же состоянием динамической системы . Следовательно, существует векторная функция, которую мы, следуя Такенсу, обозначим , отображающая вектора в точку m-мерного евклидового пространства ,

.

То есть мы пришли к ситуации, описанной в условиях теоремы Уитни, где роль отображения g играет , а роль многообразия - . В теореме предполагается, что , h и по крайней мере дважды дифференцируемы, а для всех неподвижных точек и циклов с периодами , предполагается, что у них все собственные значения простые и не равны 1, а h(x) для них различны. Тогда теорема Такенса утверждает, что типичным свойством отображения будет то, что при оно будет давать вложение многообразия в :

Теорема 1 (Такенс). Пусть M – компактное многообразие размерности d. Для пар , , является типичным свойством, что отображение определённое как

является вложением.

Теорема Такенса подводит строгую математическую основу под идеи нелинейной регрессии. После работ Такенса почти те же идеи фигурируют под другими названиями – реконструкция аттрактора, фазового пространства, динамической системы, и т.п.