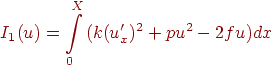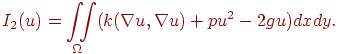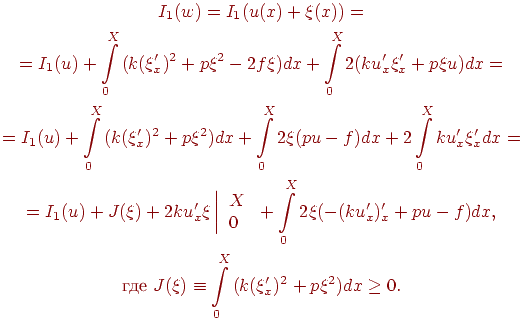67. Метод Ритца.
Рассмотрим две задачи:
|
(7.1) |
|
|
|
(7.2) |
||
Эти задачи похожи: (7.1) является одномерным случаем более общей задачи (7.2). Уравнения (7.1) и (7.2) записаны в самосопряженной форме. Поставим задачам (7.1) и (7.2) в соответствие функционалы
|
(7.3) |
и
|
(7.4) |
Будем
рассматривать пространство функций
(пространство
Соболева) с нормой
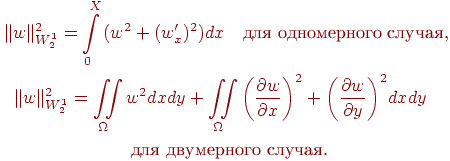
Это — функции с ограниченным интегралом.
Теорема
5.
Среди всех функций
удовлетворяющих
граничным условиям, решение задачи
(7.1) придает наименьшее значение
функционалу (7.3), а решение (7.2) — функционалу
(7.4).
Доказательство.
Докажем это утверждение для одномерного случая, а доказательство для уравнений (7.2), (7.4) оставим в качестве упражнений.
Введем
Поскольку
а
u(x) — дважды непрерывно дифференцируемая
функция, то
и
ξ(0) = ξ(X) = 0.
|
(7.5) |
Третье
слагаемое в (7.5) равно нулю в силу граничных
условий для функции ξ;
последнее слагаемое равно нулю, так как
u
— решение (7.1); второе слагаемое —
неотрицательное. Следовательно, минимум
функционала I1(w)
достигается, когда J(ξ)
= 0, т.
е.
или,
что то же самое, w(x)
= u(x) .
Чуть сложнее эта теорема доказывается для двумерного случая, где надо воспользоваться теоремой Остроградского - Гаусса. Таким образом, решение соответствующей задачи в частных производных (7.2) или краевой задачи для ОДУ (7.1) сводится к задаче минимизации некоторого функционала.
В том случае, если функционал (7.3) или (7.4) ограничен снизу, то экстремаль функционала — минимум, и численный метод, который будет построен ниже, носит название метода Ритца. Чаще, когда нет необходимости тщательно исследовать постановку задачи, говорят об экстремальной точке, стационарной точке функционала и т.д.
81. Минимизируемые функционалы. Пространства Соболева.
|
(7.4) |
Будем рассматривать пространство функций (пространство Соболева) с нормой
Это — функции с ограниченным интегралом.
Теорема 5. Среди всех функций удовлетворяющих граничным условиям, решение задачи (7.1) придает наименьшее значение функционалу (7.3), а решение (7.2) — функционалу (7.4).
73. Метод Канторовича.
74. Метод Куранта.
48. Метод Трефтца.
