19. Система Ван-дер-Поля.

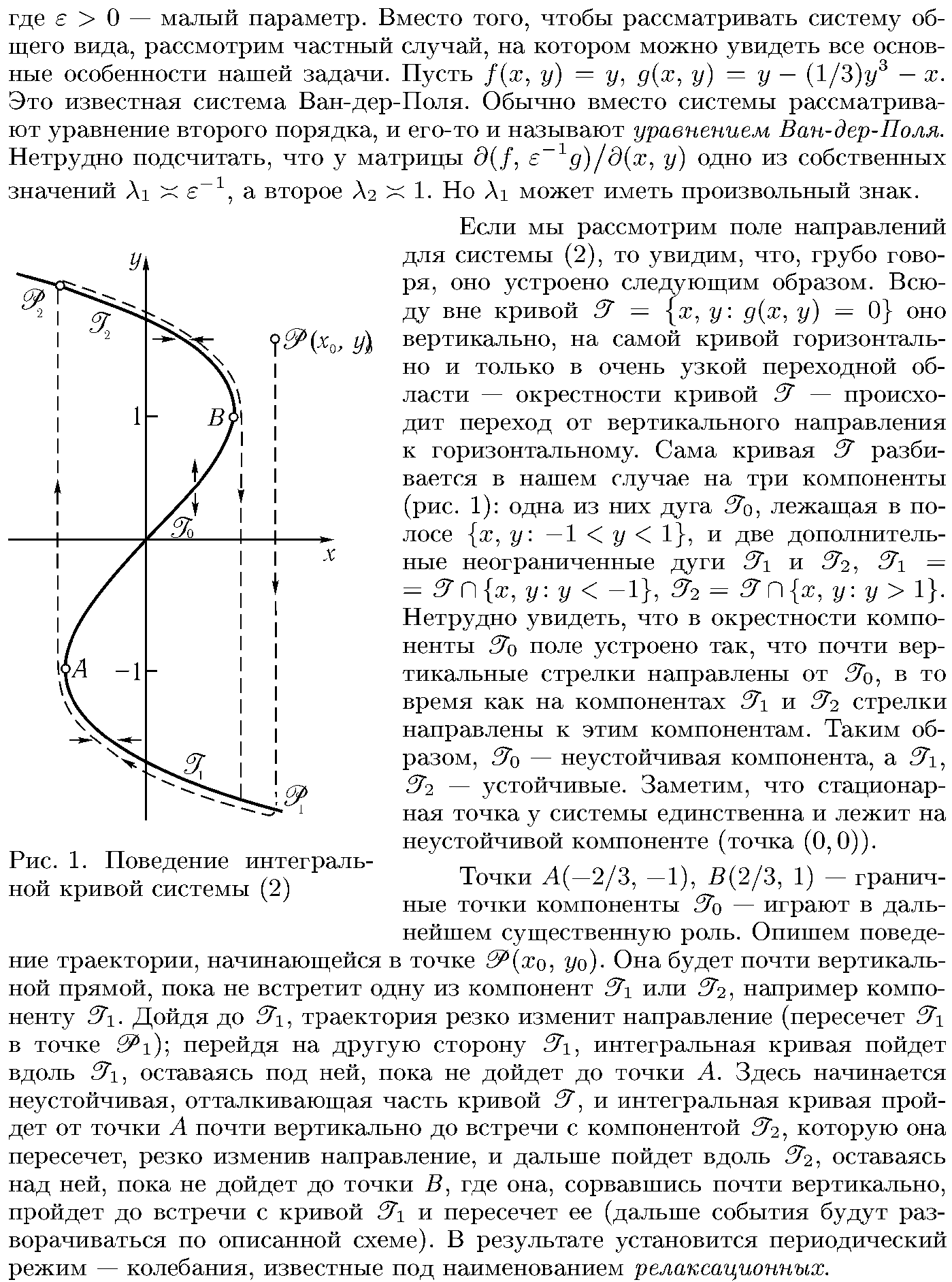
21. Метод Розенброка.

Одноитерационные методы Розенброка. Розенброком был предложен класс неявных методов, в котором не решается система нелинейных уравнений. В простейшем случае для автономной системы уравнений методы типа Розенброка могут иметь вид [9.3]

Здесь

матрица, постоянная на данном шаге по времени. Параметры a, b, c подбираются таким образом, чтобы обеспечить максимально возможный порядок точности.

Например, для схемы третьего порядка точности получим

a = 1, 077; b = - 0, 372; c = - 0, 577 .

Такую схему иногда называют методом с одной итерацией, имея в виду, что вычисление обратной матрицы сравнимо по количеству арифметических операций с одной итерацией метода Ньютона. Преимущество методов типа Розенброка перед прочими классами численных методов Жестких Сиситем ОДУ заключается в том, что для определения решения на верхнем временном слое необходимо решать уже линейную систему алгебраических уравнений.

22. Метод Нумерова.

Пусть краевая задача имеет вид

(10.3)

где нелинейная функция f не зависит явно от первой производной y'_x. В 1924 году Б.Нумеров предложил следующий метод аппроксимации задачи (10.3):

(10.4)

где введено обозначениеf_k = f(x_k, y_k).

В чем заключается отличие метода Нумерова от аппроксимации вида (10.5):

(10.5)

Описать алгоритмы численного решения нелинейных алгебраических систем (10.4) и (10.5). В случае (10.4) и f = f(x) это — алгоритм прогонки.

Решение. Выпишем главный член погрешности аппроксимации разностного уравнения (10.4). Для этого подставим в разностное уравнение проекцию на сетку точного решения задачи (10.3). Следует отметить, что конкретный вид решения не важен, достаточно только, чтобы решение существовало. Предположим также, что оно четырежды непрерывно дифференцируемо.

Раскладывая проекции точного решения в правой части (10.4) в ряд Тейлора до четвертого порядка включительно, убедимся, что все нечетные производные взаимно уничтожатся, а четные дадут следующее выражение для главного члена погрешности аппроксимации:

Из уравнения (10.3) следует, что во всех внутренних точках области выполняется равенство

переходя в последнем равенстве к разностной аппроксимации правой части, можно учесть явно главный член погрешности аппроксимации в (10.5). Приводя подобные слагаемые в (10.4), получаем аппроксимацию Нумерова

которая приближает исходную задачу во внутренних точках сеточной области с четвертым порядком.

Такая идея разумного распоряжения правой частью для неоднородных и нелинейных задач приводит к компактным (возможно, название не слишком удачное — термины "компакт" и "компактный" уже давно заняты в математике под совсем другое!) разностным схемам — схемам повышенного порядка точности на нерасширенном шаблоне. Действительно, и в элементарном шаге вычислений для (10.4) и (10.5) участвуют только три точки. Вопросам построения компактных разностных схем для нелинейных уравнений в частных производных посвящена монография [10.7].

В случае, когда правая часть явно зависит от первой производной, либо не получается компактной схемы, либо схема перестает быть экономичной. Действительно, чтобы не ухудшить порядок аппроксимации, необходимо вычислять значение первой производной в соответствующих узлах со вторым порядком. Если во всех точках использовать формулу с центральной разностью, то расширится шаблон схемы — в каждом шаге элементарных вычислений должно теперь участвовать пять точек. Если для точки с индексом n использовать формулу с центральной разностью, а для точек с индексами n + 1 и n - 1 — соответствующие формулы для односторонней производной, то для каждой точки шаблона придется вычислять заново значения функции f. При использовании классического вида аппроксимации Нумерова при каждом элементарном вычислении производится лишь однократное обращение к функции вычисления правой части — лишь для f_{n + 1}, значения f_n и f_{n - 1} уже получены при вычислениях для точки с индексом n - 1. Так как время вычислений, как правило, определяется в таких задачах именно количеством обращений к правой части, то вычисления замедляются в три раза.