17. Шаблоны. Явные и неявные шаблоны.

Явная разностная схема для приближенного решения уравнения теплопроводности во внутренних узлах сетки (не принадлежащим границе сеточной области) имеет вид

Под разностной схемой понимается совокупность разностных уравнений для определения значений сеточной функции внутри расчетной области, дополненная соответствующими начальными и граничными условиями для этой сеточной функции. Шаблон схемы, представляющий собой конфигурацию расчетных узлов в области интегрирования, используемых на каждом элементарном шаге вычислений , показан на рис. 1.2.

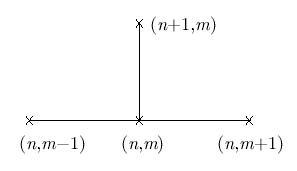
Рис. 1.2. 

Эта схема аппроксимирует дифференциальное уравнение во внутренних точках (узлах) области интегрирования, т.е. при n = 1 , ... , N - 1, m = 1 , ... , M - 1. Проведем аппроксимацию начальных данных и краевых условий:

для определенности положим

Расчет ведется по рекуррентной формуле на каждом временном слое от n = 1 до n = N от m = 1 до m = M - 1 во внутренних узлах; слой n = 0(t = t₀) соответствует начальным данным, лучи m = 0(x = x₀) и m = M(x = x_M) — левому и правому краевым условиям.

Запишем явную схему в виде

По этой формуле последовательно, на каждом слое вычисляется сеточная функция во внутренних узлах области интегрирования.

Для завершения расчета слоя t = t_{n + 1} необходимо вычислить и для чего разрешаем левое и правое краевые условия относительно этих величин:

где и уже вычислены ранее. Реализация одного шага по времени занимает O(M) арифметических операций , всех слоев — O(NM) операций.

Явными схемами называются такие разностные схемы для эволюционных уравнений , когда данные на следующем слое по времени находятся непосредственно из данных на предыдущем слое без решения алгебраических систем уравнений. Если же на верхнем временном слое для определения значений сеточной функции необходимо решать систему алгебраических уравнений , то схема называется неявной.

Простейшая неявная разностная схема имеет вид (для простоты положим a = 1)

ее шаблон (рис. 1.3).

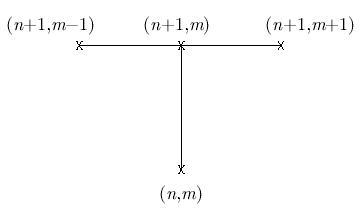
Рис. 1.3. 

18. Теорема Лакса-Рябенького. Аппроксимационность. Устойчивость.

К сожалению, чтобы исследовать схему на сходимость, необходимо знать точное решение дифференциальной задачи. Обычно разностные схемы исследуются на аппроксимацию и устойчивость, откуда по теореме П.Лакса и В.С.Рябенького и следует сходимость, по крайней мере, для линейных задач.

Пример разностной задачи, аппроксимирующей рассматриваемое уравнение:

Можно показать, получив общее решение разностной задачи, что эта схема не является устойчивой и, следовательно, не имеет место сходимость решения к точному решению дифференциальной задачи.

Определение 2. Говорят, что разностная задача аппроксимирует дифференциальную на ее решении, если норма невязки, возникающей при действии разностного оператора на сеточную функцию — проекцию на сетку точного решения

стремится к нулю при если выполнена оценка , (константа, входящая в правую часть неравенства, не зависит от сеточных параметров), то имеет место аппроксимация порядка p.

Определение 3. Говорят, что разностная задача является устойчивой, если из соотношений

следует в смысле выбранной нормы

Теорема (П. Лакса - В.С.Рябенького). Решение линейной разностной задачи сходится к решению дифференциальной , если разностная задача устойчива и аппроксимирует дифференциальную задачу на ее решении. При этом порядок аппроксимации совпадает с порядком сходимости.

Дадим еще одно эквивалентное определение устойчивости разностной задачи, применимое лишь для линейных разностных операторов. Как будет видно ниже, даже для линейных дифференциальных задач возможно построение нелинейных разностных схем.

Определение 4. Линейная разностная задача устойчива, если при любой правой части F_τ она имеет единственное решение u_τ, причем и данная оценка равномерна по сеточным параметрам .