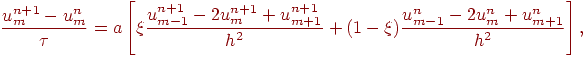29. Условие Куранта, Фридрихса, Леви. Область зависимости.

Рассмотрим разностное уравнение

аппроксимирующее задачу Коши для уравнения переноса

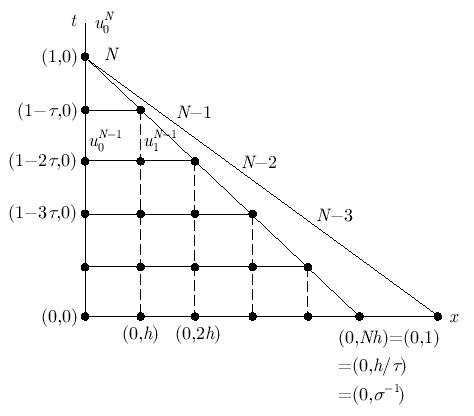
Рис. 1.4. 

Очевидно, что значение сеточной функции в точке (1, 0) выражается через значения и в точках (1 - τ, 0), (1 - τ, h). В свою очередь, значения и находятся по значениям сеточной функции в точках (1 - 2τ, 0), (1 - 2τ, h), (1 - 2τ, 2h), значения сеточной функции находятся по значениям в точках (1 - 3τ, ih), i = 0, ... , 3 , и т.д. Значение сеточной функции выражается через значение решения в точках расчетной сетки (0, mh), m = 0, ... , N , N = τ ^{- 1} Все эти точки лежат на отрезке [0, h/τ] или [0, σ ^{- 1}] оси t = 0, на которой задано начальное условие исходной дифференциальной задачи. Значение не зависит от значения функции при x, лежащих вне отрезка [0, σ ^{- 1}].

Из курса обыкновенных дифференциальных уравнений известно, что решением однородного уравнения переноса является функция сохраняющая свое значение вдоль характеристики t + x = const, и, в частности, на прямой t + x = 1, проходящей через точки (1, 0), (0, 1) , см. рис. 1.4.

Таким образом, при σ > 1 область зависимости решения дифференциальной задачи для являющаяся точкой (0, 1), не входит в отрезок В случае σ ^{- 1} < 1 и сходимость решения разностной задачи к решению дифференциальной отсутствует. Разумеется, приведенные рассуждения не носят характера доказательства, а лишь косвенно объясняют, почему не следует ожидать сходимости при σ = τ/σ > 1.

Сформулируем теперь условие Куранта - Фридрихса - Леви (условие КФЛ), необходимое для сходимости разностной задачи.

Пусть некая точка A принадлежит области определения решения u(t , x) и значение функции u(A) зависит от значения некоторой функции в точках x, принадлежащих множеству Ω(A), которое, в свою очередь, принадлежит области определения функции .

Положим, что для приближенного вычисления решения уравнения используется разностная схема , причем, значение решения в точке A_x расчетной сетки, ближайшей к A, полностью определяются значениями функции на множестве Ω_x(A_x). Для того чтобы имела место сходимость при , разностная схема должна быть устроена так, чтобы при сколь угодно малых значениях пространственного шага h в произвольной окрестности любой точки области Ω(A) имелась точка множества Ω_x(A_x).

Другими словами, разностная схема должна быть устроена так, чтобы область зависимости разностного уравнения учитывала область зависимости решения исходного дифференциального уравнения. В противном случае сходимости ожидать, вообще говоря, нельзя. Если же разностная задача аппроксимирует дифференциальную, то необходимое условие сходимости КФЛ является также необходимым условием устойчивости схемы. Отметим, что условию КФЛ можно придать форму теоремы.

20. Решение уравнения параболического типа. Метод сеток.

Рассмотрим численные методы решения уравнений параболического типа.

Одномерное линейное уравнение теплопроводности (диффузии). Напомним постановку соответствующей смешанной задачи:

(2.1)

Здесь a = a(x, t) > 0. Для того чтобы задача была поставлена корректно, необходимо задать начальное условие

u(0, x) = u₀(x), t = 0,

и граничные условия

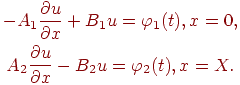
О свойствах решений линейного уравнения теплопроводности подробнее в [12.1], [12.3].

Одномерное квазилинейное уравнение теплопроводности (диффузии):

(2.2)

Уравнения такого вида встречаются в теории горения, астрофизике, физике плазмы, теории сверхпроводимости Гинзбурга - Ландау, динамике популяций и других приложениях. Здесь a(u) > 0 при любых значениях u, кроме того, . Для глобальной ограниченности решения также требуется выполнение условия

Для корректной постановки задачи необходимо задать одно начальное и два граничных условия. Подробнее о квазилинейных уравнениях теплопроводности в книгах [12.4], [12.5], [12.6], [12.7], [12.8].

Двухмерное линейное уравнение теплопроводности (диффузии):

(2.3)

Для численного решения уравнения (2.1), по - видимому, наиболее известной является параметрическая двухслойная шеститочечная разностная схема вида

(2.4)

где

При ξ = 0 имеем явную схему

устойчивую при

с порядком аппроксимации O(τ, h²) .

При ξ = 1 имеем неявную схему

устойчивую при любых τ, h, с порядком аппроксимации O(τ, h²).

При ξ = 1/2 разностный метод называется схемой Кранка - Никольсон:

Схема устойчива при любых шагах τ, h и имеет порядок аппроксимации O(τ², h²). Эта схема, в отличие от двух предыдущих, не является монотонной, т.е. она может давать осцилляции разностного происхождения на решениях, имеющих большие градиенты.