30. Исследование устойчивости уравнения параболического типа методом Фурье.

Простейшая явная разностная схема для численного решения двумерного уравнения теплопроводности

получается путем замены производных конечными разностями

или, в операторной форме,

Исследование спектральной устойчивости этот схемы ( ) приводит к следующему результату для спектра оператора послойного перехода:

откуда получаем условие устойчивости

Для неявной схемы

исследование на устойчивость по спектральному признаку дает

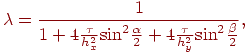
т.е. схема устойчива при любых .

Приведем исследование спектральной устойчивости для схемы переменных направлений.

Рассмотрим переход с нижнего на верхний временный слой. В таком случае можно положить ; сомножитель λⁿ опускаем, так как рассматривается один переход с n - го на (n + 1) - й слой в предположении, что известно решение на n - ом слое (можно было бы написать, , где C = λⁿ, но в этом нет смысла, так как C в дальнейших выкладках сократится).

Тогда на первом этапе получим , а на втором —

Вычисление λ₁ и λ₂ дает

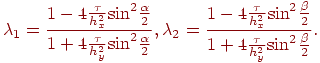
Окончательно спектр оператора послойного перехода представим в виде произведения спектров на каждом промежуточном этапе.

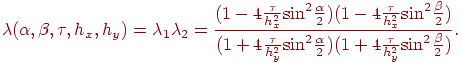
Схема безусловно устойчива.

34. Схема Кранка-Никольсон.

При ξ = 1/2 разностный метод называется схемой Кранка - Никольсон:

Схема устойчива при любых шагах τ, h и имеет порядок аппроксимации O(τ², h²). Эта схема, в отличие от двух предыдущих, не является монотонной, т.е. она может давать осцилляции разностного происхождения на решениях, имеющих большие градиенты.

38. Метод дробных шагов.

Численное решение даже простейших уравнений параболического типа сильно усложняется, если в задаче имеется в наличии более одного пространственного измерения. Условие устойчивости для многомерных схем накладывает столь жесткие ограничения на шаги по времени, что расчет по ним практически невозможен. Необходимо применять неявные схемы. Представим разностную схему для численного решения двумерного уравнения теплопроводности

в виде

здесь

Получена линейная система с разреженной (блочной) матрицей. Однако вид этой матрицы таков, что алгоритм пятиточечной прогонки в данном случае не применим.

Можно предложить схему расщепления по направлениям, или локально - одномерную схему (метод дробных шагов, Н.Н.Яненко [12.7]):

Соответствующий пространственный шаблон схемы будет

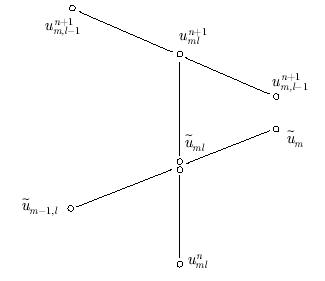
Рис. 2.3. 

Для аналогичной трехмерной задачи

можно предложить локально - одномерную схему дробных шагов

Порядок аппроксимации этих схем: в двумерном случае и — в трехмерном.Порядок аппроксимации этой схемы по времени можно увеличить до второго, если провести усреднение операторов аппроксимирующих вторые производные по координатам x_i (i = 1 ÷ 3) :

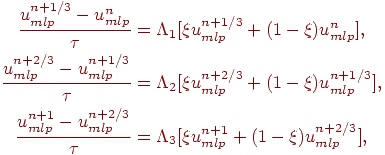
где причем при ξ = 1/2 порядок аппроксимации схемы будет Эта схема Кранка - Никольсон устойчива при любых τ, h_x, h_y, h_z; ее шаблон для двумерной задачи

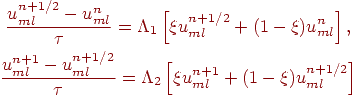
представлен на рисунке.

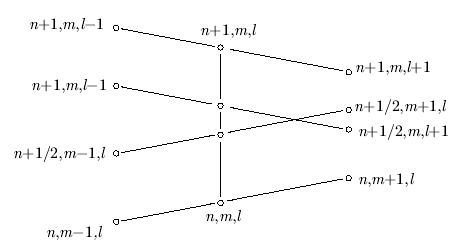
Рис. 2.4. 

39. Схема Дугласа-Ганна.

Схема Дугласа - Ганна — это общий метод построения неявных разностных схем переменных направлений для трехмерного уравнения теплопроводности, имеющих второй порядок точности и безусловно устойчивых [12.13]:

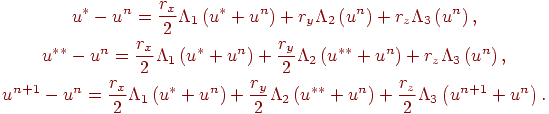
Верхние индексы * и ** обозначают промежуточные значения, координатные индексы i, j, k опущены во всех членах уравнений, — компоненты разностного оператора теплопроводности. На каждом шаге метода возникает система линейных уравнений с трехдиагональной матрицей, решаемая методом прогонки. Схема Дугласа - Ганна безусловно устойчивая. В настоящее время это наиболее удачная из схем расщепления в трехмерном случае.

25. Решение уравнения гиперболического типа.

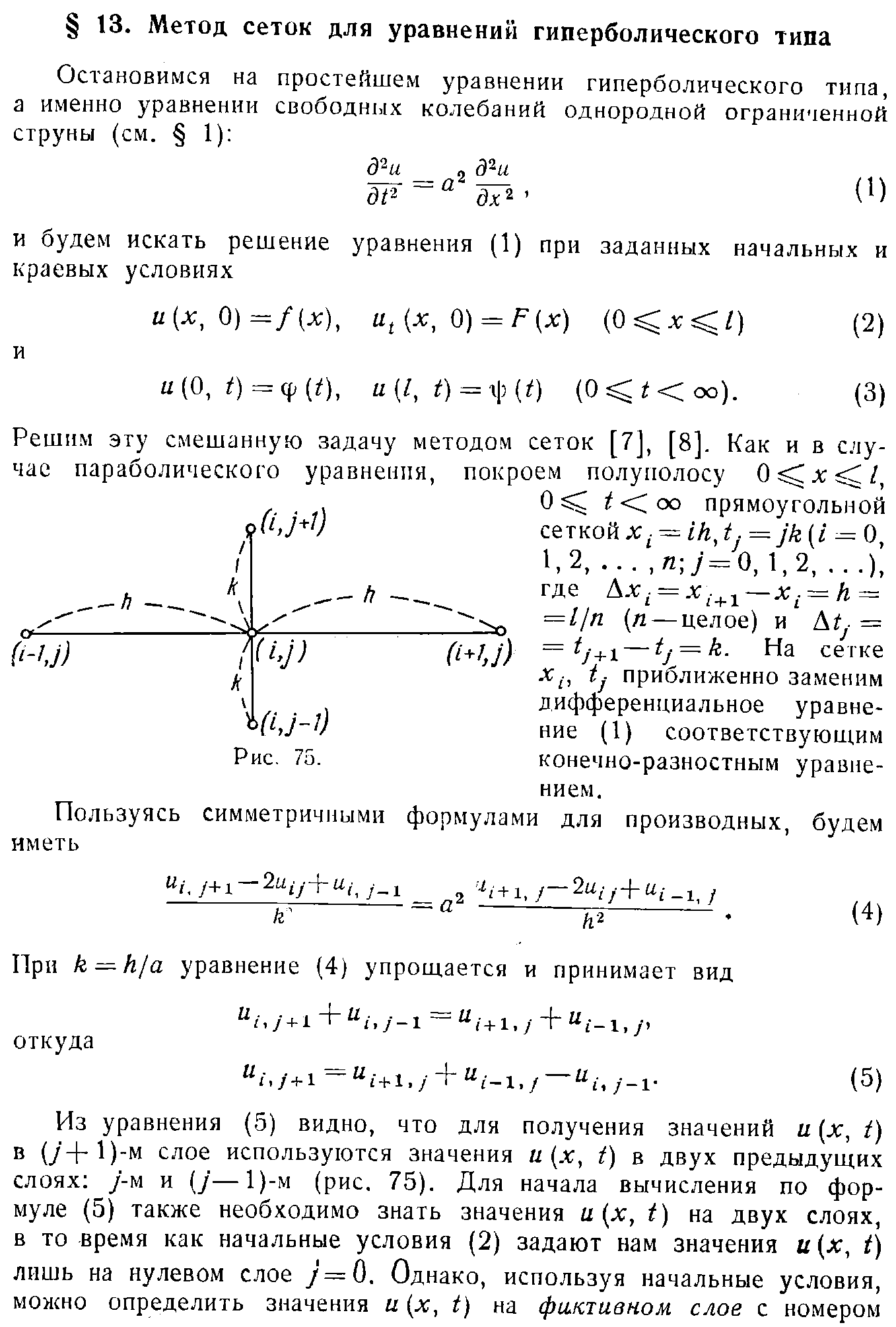
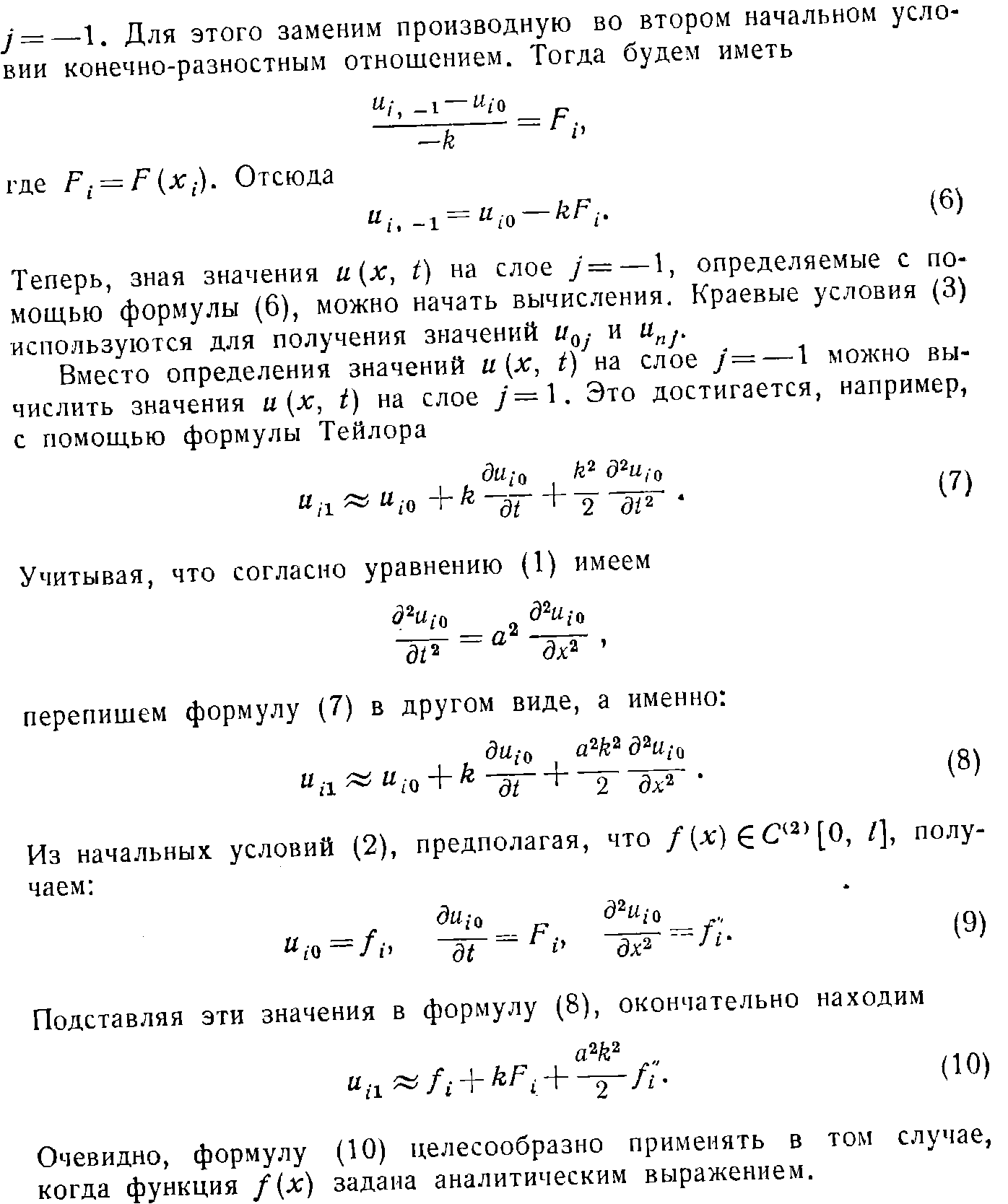
44. Метод Массо для уравнения 1 порядка.

45. Характеристики метода Массо для гиперболического уравнения 2 порядка.

41. Монотонность метода.

Кроме основных понятий теории разностных схем — аппроксимации, устойчивости, сходимости — на практике существенную роль играют дополнительные свойства разностных схем. Среди таких свойств упомянем монотонность. Не существует общепринятого определения монотонности разностной схемы. Пока, до рассмотрения разностных схем в пространстве неопределенных коэффициентов, воспользуемся определением, данным Борисом и Буком в [13.5], [13.6].

Под монотонными далее будем понимать такие разностные схемы, в которых не увеличивается число локальных экстремумов (минимумов и максимумов численного решения) по сравнению с числом локальных экстремумов в решении точной задачи. Кроме того, монотонные схемы не должны увеличивать по абсолютному значению уже имеющиеся экстремумы.

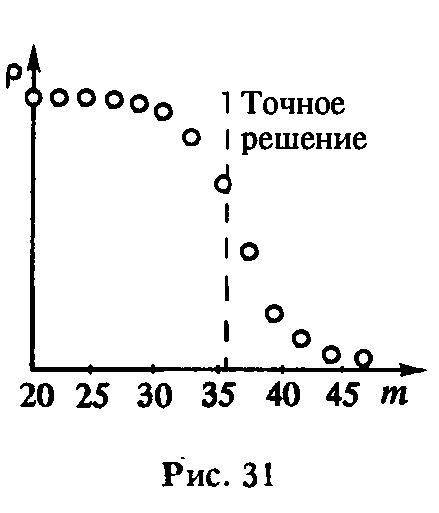
Свойство монотонности разностной схемы очень полезно при расчете разрывных решений. К сожалению, доказанная для линейного уравнения переноса теорема С.К.Годунова гласит, что среди линейных разностных схем (термин "линейный" уточним чуть ниже) не существует монотонных с порядком аппроксимации выше первого.

Зачастую в практических задачах схемы первого порядка аппроксимации не могут обеспечить требуемую точность численного решения.

При использовании немонотонных схем для получения численных решений с большими градиентами, появляются осцилляции разностного происхождения. По этой причине в численных методах часто используется регуляризация численных решений. Рассмотрим наиболее распространенные методы регуляризации.

42. Теорема Годунова.

См. Выше

62. Гибридные методы.

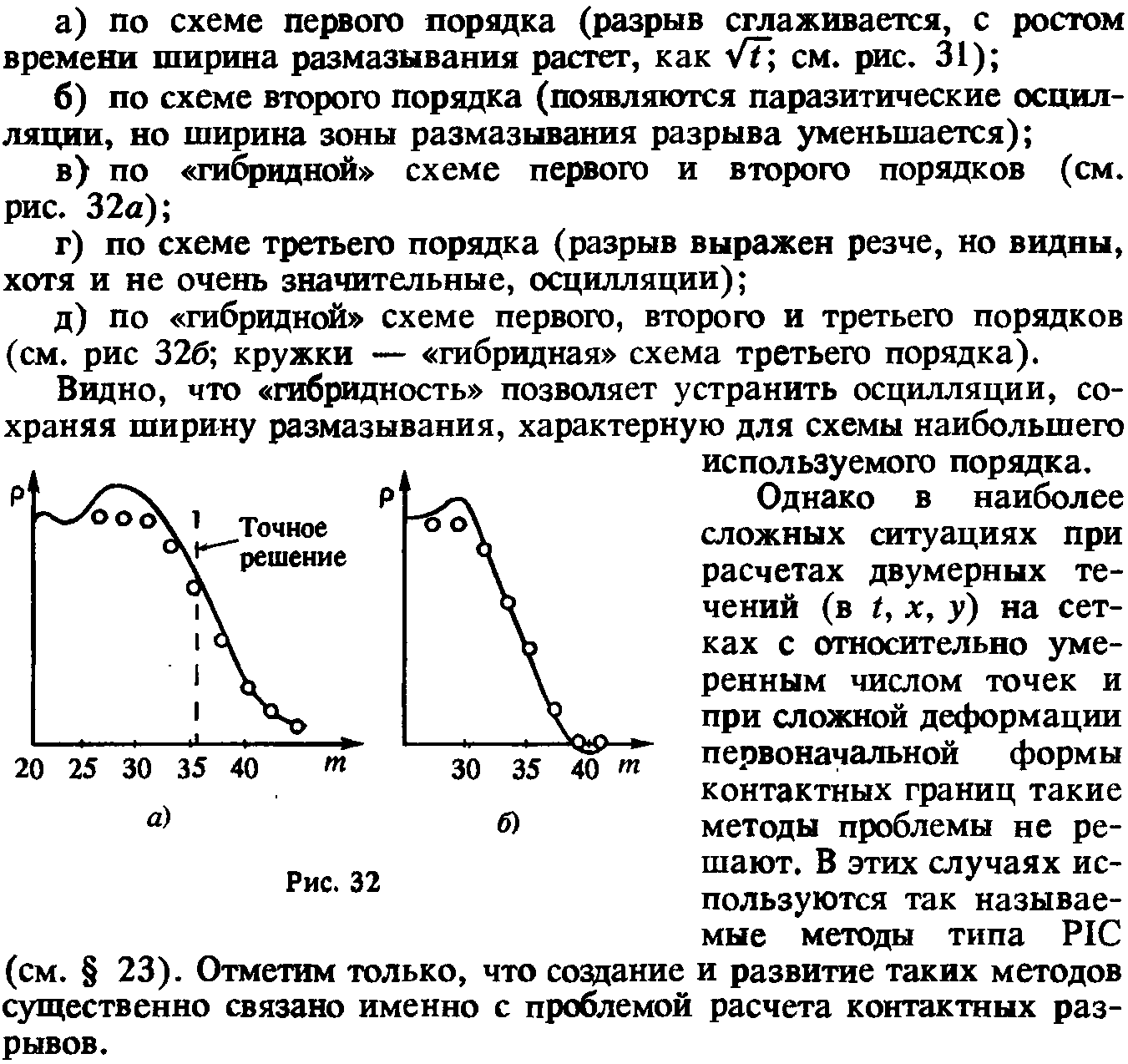
33. Аппроксимация граничных условий в уравнениях эллиптического типа.

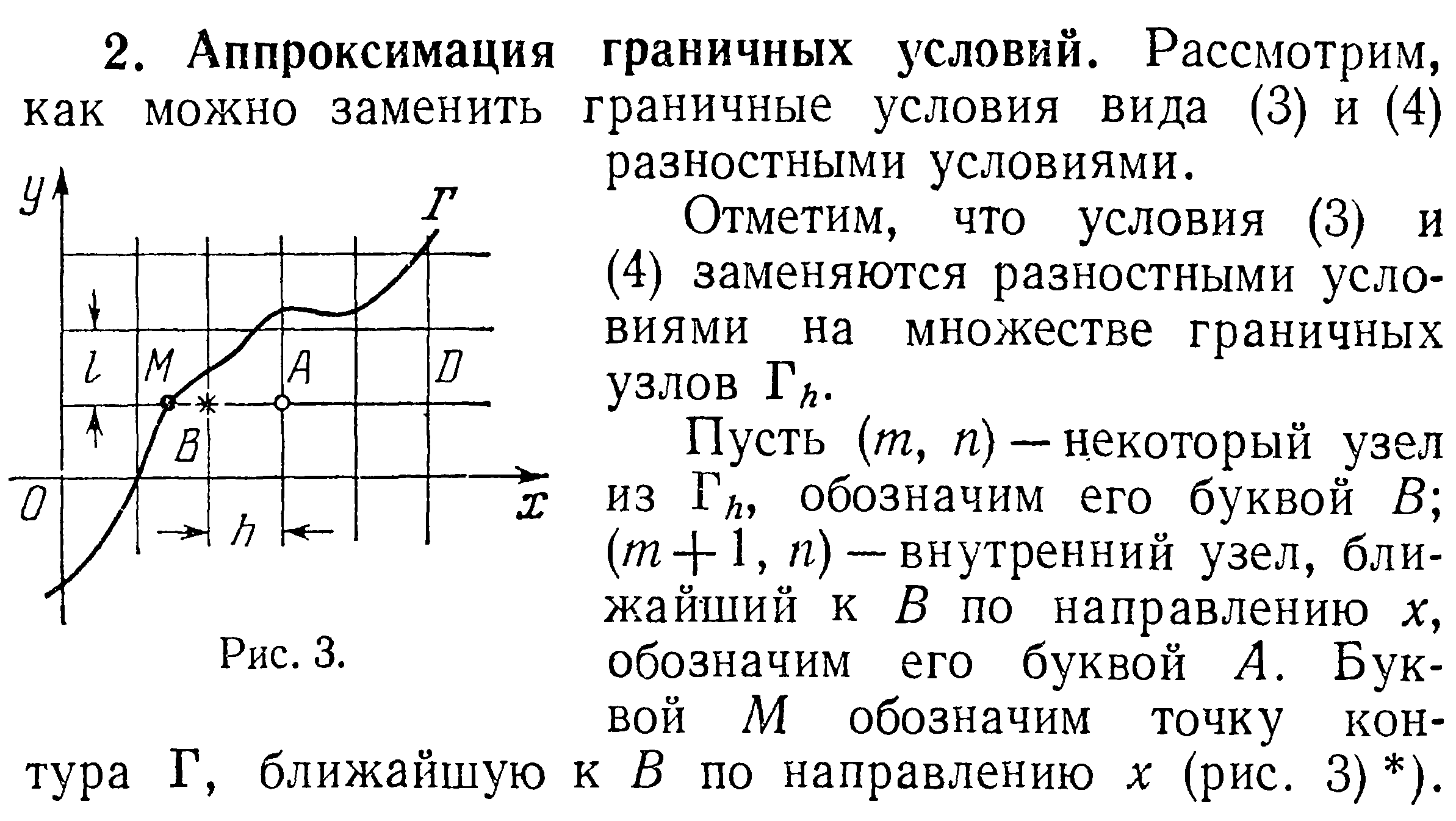
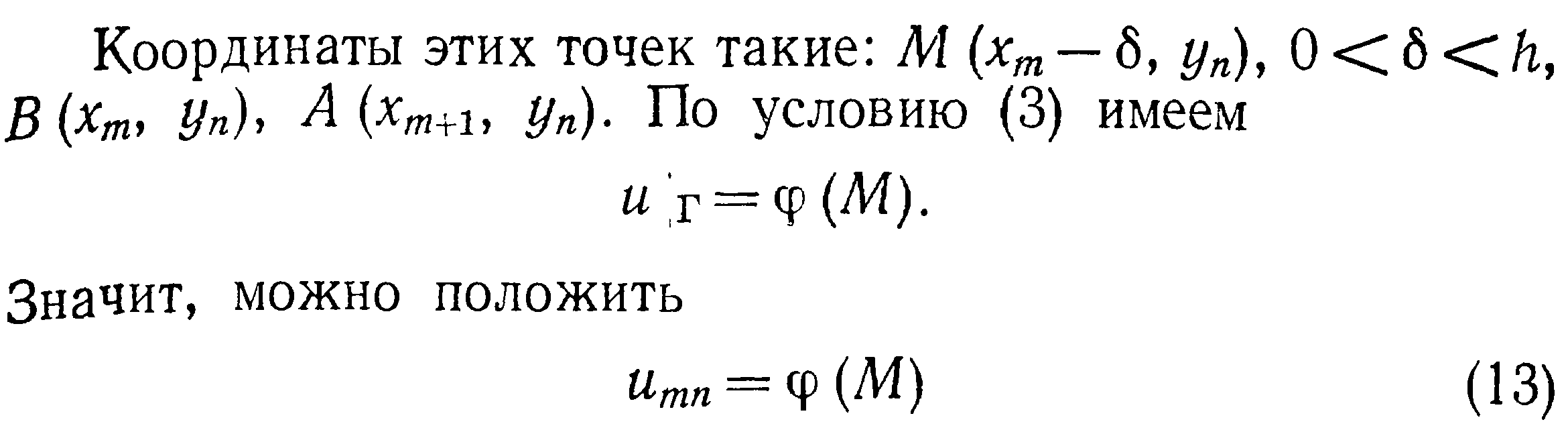
56. Итерации при решении уравнений эллиптического типа. Чебышевское ускорение сходимости.

Рассмотрим итерационный метод с выбором параметра τ на каждой итерации:

Соответствующие соотношения для эволюции невязки имеют вид:

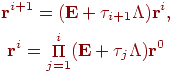
После разложения невязок на двух соседних итерациях по базису из собственных функций сеточного оператора получим равенство

Для коэффициентов разложения и компонентов невязки справедливы следующие равенства:

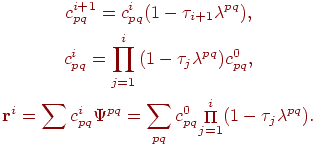
Оценим погрешности на i шаге итераций

Вновь приходим к минимаксной задаче: найти такую последовательность итерационных параметров чтобы выполнялось

Заметим, что есть полином (относительно τ) степени i. Задача — сделать его наименее уклоняющимся от нуля на отрезке [l, L]. Эта задача, как известно, решена Чебышевым, а корни этого полинома являются нулями полинома Чебышева:

Достаточно громоздкие выкладки, которые опускаются, дают в результате оценку скорости сходимости метода с оптимальным набором параметров и числа итераций, необходимого для достижения заданной точности

Трехслойный метод Чебышева можно также представить в следующем виде:

где

Трехслойный метод Чебышева в настоящее время применяется значительно чаще двухслойного при численном решении уравнений эллиптического типа.