7) Повторение испытаний. Формула Бернулли.

Несколько опытов называются независимыми, если вероятность исхода опыта не зависит от того, какие исходы имели другие опыты. Рассмотрим случай, когда вероятности исходов опытов постоянны и не зависят от номера опыта.

Пусть один тот же опыт проводятся n раз. В каждом опыте некоторые события А₁, А₂, …, А_r появляется с вероятностями р_1, р₂, …, р_п. Будем рассматривать не результат каждого конкретного опыта, а общее число появлений событий А₁, А₂, …, А_r .

Рассмотрим случай с двумя возможными исходами опытов, т.е. в результате каждого опыта событие A появляется с вероятностью р и не появляется с вероятностью q=1-p. 

Вероятность P(n,k) того, что в последовательности из n опытов интересующее нас событие произойдет ровно k раз (безразлично, в какой последовательности), равна (формула Бернулли)

Следствия из формулы Бернулли.

1. Вероятность того, что событие А наступит менее k раз

2. Вероятность того, что событие наступит более k раз

3. Вероятность того, что в n опытах событие А появится от k1 до k2 раз

. (4.4)

4. Вероятность того, что в n опытах событие А появится хотя бы один раз

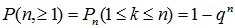
Число к₀, которому соответствует максимальная биномиальная вероятность  , называется наивероятнейшим числом появления события А. При заданных n и p это число определяется неравенствами:  .

 

8) Функция Лапсласа. Свойства функции.

Функция Лапласа (функция ошибок) не выражается через элементарные функции  .

Для ее вычисления используются специальные таблицы или методы приближенного вычисления.

Функция   обладает следующими свойствами:

; ;

= –  , функция   – нечетная, поэтому в таблицах обычно приводятся значения   только для положительных  ;

, функция   – монотонно возрастающая.  При  , с точностью до тысячных можно принять 

10). Формула Пуассона.Связь между формулами Пуассона и Бернулли.

При большом числе испытаний n  и малой вероятности р формулой Бернулли пользоваться неудобно, например,   вычислить трудно. В этом случае для вычисления вероятности того, что в n  испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона:

 – среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для   и  .

9) Локальная и интегральная теоремы Лапласа.

Теоремы Муавра-Лапласа. На практике приближенные формулы Муавра-Лапласа применяются в случае, когда p и q не малы , а npq>9.

Локальная теорема Муавра-Лапласа. Если вероятность появления события А в каждом из n  независимых испытаний равна одной и той же постоянной р=const (0<р<1), то вероятность   того, что во всех этих испытаниях событие А появится ровно k раз, приближенно вычисляется формулой:

где:   ,  -- кривая Гаусса.

Таблицы значений функции   даны в приложениях к учебникам по теории вероятностей

Интегральная теорема Муавра-Лапласа. Пусть вероятность появления события А в каждом из n (n→∞) независимых испытаний равна одной и той же постоянной р (0<р<1), то вероятность   того, что во всех этих испытаниях событие А появится не менее k₁ и не более k₂ раз, приближенно вычисляется формулой:

Где  - функция Лапласа,

, 

Значения аргументов функции Лапласа для х Î[0,5] даны в приложениях к учебникам по теории вероятностей (Приложение 2 настоящего методического пособия), для x>5 F(x)=1/2.Функция нечетная - F(x)= F(-x).

11).Дискретные случайные величины. Характеристики Д.С.В.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены. Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Закон распределения дискретной случайной величины можно задать таблично, в виде формулы (аналитически) и графически.

Числовые характеристики дискретных случайных величин

Числа, которые описывают случайную величину суммарно, называют числовыми характеристиками случайной величины. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности: , где   – возможные значения случайной величины  , а   – соответствующие вероятности. Замечание. Вышеприведенная формула справедлива для дискретной случайной величины, число возможных значений которой конечно. Если же случайная величина имеет счетное число возможных значений, то для нахождения математического ожидания используют формулу: , причем это математическое ожидание существует при выполнении соответствующего условия сходимости числового ряда в правой части равенства. Вероятностный смысл математического ожидания: математическое ожидание приближенно равно (тем точнее, чем больше число испытаний) среднему арифметическому наблюдаемых значений случайной величины.

12).Свойства математического ожидания и дисперсии д.с.в.

1. Мат. ожидание постоянной величины равно самой постоянной: . 2. Постоянный множитель можно вынести за знак математического ожидания: . 3. Мат. ожидание произведения двух независимых сл, величин равно произведению их мат. ожиданий: . Следствие. Мат/ожидание произведения нескольких взаимно независимых сл, величин равно произведению их мат. ожиданий. 4. Мат. ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: Следствие. Мат.ожидание суммы нескольких сл. величин равно сумме мат. ожиданий слагаемых.

Пусть производится   независимых испытаний, в каждом из которых вероятность появления события   постоянна и равна  . Тогда справедлива следующая теорема. Теорема. Мат/ожидание числа появлений события   в   независимых испытаниях равно произведению числа испытаний на вероятность появления этого события в каждом испытании: .

Отклонение- это разность между сл. величиной и ее мат.ожиданием Теорема. Мат. ожидание отклонения равно нулю: .

Дисперсией дискретной сл.величины называют мат ожидание квадрата отклонения сл. величиной от ее мат ожидания: Дисперсия имеет размерность, равную квадрату размерности сл/величины. Теорема. Дисперсия равна разности между мат. ожиданием квадрата случайной величины   и квадратом ее мат ожидания:

Свойства дисперсии

1. Дисперсия постоянной величины равно нулю: . 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: . 3. Дисперсия суммы двух независимых сл. величин равно сумме дисперсий этих случайных величин: . Следствие. Дисперсия суммы нескольких взаимно независимых сл. величин равно сумме дисперсий этих величин. 4. Дисперсия разности двух независимых сл. величин равно сумме дисперсий этих случайных величин: .

Теорема. Дисперсия числа появлений события   в   независимых испытаниях, в каждом из которых вероятность   появления события постоянна, равна произведению числа испытаний на вероятность   появления и вероятность   непоявления этого события в одном испытании: .

Средним квадратическим отклонением сл.величины называют квадратный корень из дисперсии: . Размерность среднего квадратического отклонения совпадает с размерностью самой сл.величины.