25) Вероятность попадания нормально распределённой с.В. В интервал.

Определим вероятность попадания нормально распределенной случайной величины в интервал от α до β:

Сделав замену переменной t=(x-m)/σ, получим:

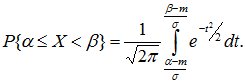
Так как первообразная для e^-x не выражается через элементарные функции, то для вычисления вероятностей событий, связанных с нормальными случайными величинами используют табулированную функцию Лапласа:

.

С помощью этой функции вероятность попадания нормально распределенной случайной величины на интервал от α до β определится так:

где  m – математическое ожидание, 

 – среднее квадратическое отклонение данной с.в.

Функция Лапласа обладает следующими свойствами:

1. Φ(0)=0;

2. Φ(-х)=-Φ(х);

3. Φ(-∞)=0,5.

Функция распределения нормально распределенной случайной величины через функцию Лапласа выражается так:

Нормально распределенная случайная величина возникает в тех случаях, когда складывается много независимых (или слабо зависимых) случайных величин Х₁, Х₂, …, X_n. Тогда, каковы бы не были законы распределения отдельных случайных величин X_i, закон распределения их суммы будет близок к нормальному распределению. В частности, ошибки измерений распределяются по закону, близкому к нормальному.

 

26).Вероятность отклонения нормально распределённой с.в. от среднего. Правило «трёх сигм» Вычислим вероятность того, что отклонение нормально распределенной случайной величины   от своего математического ожидания по абсолютной величине не превысит  . Воспользуемся формулой для нахождения вероятности заданного отклонения, в которую в качестве   подставим  :

Таким образом, вероятность того, что отклонение случайной величины   по абсолютной величине будет меньше утроенного среднего квадратического отклонения( ) , равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит  , составляет всего 0,0027. Это означает, что лишь в 0,27% случаев так может произойти.Такое событие, исходя их принципа невозможности маловероятных событий, можно считать практически невозможным. Вывод (правило трех сигм): если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.

27) Показательное распределение. Условие нормировки.

Непрерывная случайная величина Х, функция плотности которой задается выражением 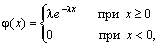      называется случайной величиной, имеющей показательное, или экспоненциальное, распределение. В отличие от нормального распределения, показательный закон определяется только одним параметром λ. В этом его преимущество, так как обычно параметры распределения заранее не известны и их приходится оценивать приближенно. Понятно, что оценить один параметр проще, чем несколько.

Найдем функцию распределения показательного закона:   Теперь можно найти вероятность попадания показательно распределенной случайной величины в интервал (а, b):      .       Значения функции е^-х можно найти из таблиц.

 Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Также этому распределению подчиняется время ожидания клиента в системе массового обслуживания (магазин, мастерская, банк, парикмахерская и т.д.). Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению.

Пусть элемент (то есть некоторое устройство) начинает работать в момент времени t₀ = 0 и должен проработать в течение периода времени t. Обозначим за Т непрерывную случайную величину – время безотказной работы элемента, тогда функция                F(t) = p(T > t) определяет вероятность отказа за время t. Следовательно, вероятность безотказной работы за это же время равна

  R(t) = p(T > t) = 1 – F(t).           Эта функция называется функцией надежности.

Часто длительность безотказной работы элемента имеет показательное распределение, то есть

                           F(t) = 1 – e^-λt .                      

Следовательно, функция надежности в этом случае имеет вид:    R(t) = 1 – F(t) = 1 – (1 – e^-λt) = e^-λt .

Показательным законом надежности называют функцию надежности, определяемую равенством

                                R(t) = e^-λt ,           где λ – интенсивность отказов.