61. Опишіть економічну і математичну постановку двохетапної транспортної задачі.

Класична транспортна задача лінійного програмування формулюється так: деякий однорідний продукт, що знаходиться у m постачальників Аі в обсягах одиниць відповідно необхідно перевезти n споживачам в обсягах одиниць. При цьому виконується умова, що загальний наявний обсяг продукції у постачальників дорівнює загальному попиту всіх споживачів. Відомі вартості перевезень одиниці продукції від кожного Аі-го постачальника до кожного Вj-го споживача, що подані як елементи матриці виду: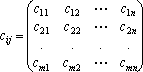

Необхідно визначити план перевезень, за якого вся продукція була б вивезена від постачальників, повністю задоволені потреби споживачів і загальна вартість всіх перевезень була б мінімальною.

У такій постановці задачі ефективність плану перевезень визначається його вартістю і така задача має назву транспортної задачі за критерієм вартості перевезень.

Запишемо її математичну модель. Позначимо через обсяг продукції, що перевозиться від постачальника до споживача . Мають виконуватися такі умови:

1. сумарний обсяг продукції, що вивозиться з кожного і-го пункту, має дорівнювати запасу продукції в даному пункті:

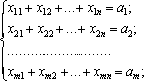
2. сумарний обсяг продукції, що ввезений кожному j-му споживачеві, має дорівнювати його потребам:

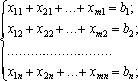
3. сумарна вартість всіх перевезень повинна бути мінімальною:

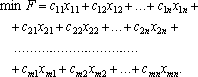Очевидно, що . У скороченій формі запису математична модель транспортної задачі за критерієм вартості перевезень має такий вигляд: (5.1).за обмежень: ; (5.2) ; (5.3) .

У розглянутій задачі має виконуватися умова: . (5.5)

У класичній постановці транспортної задачі допускається, що вантаж перевозиться безпосередньо від постачальників до споживачів. Але на практиці досить часто зустрічається випадок, коли певна частина продукції спочатку перевозиться до посередницьких фірм (сховищ), а потім споживачам. У такому разі розв’язання задачі поділяють на два етапи: спочатку знаходять оптимальний план перевезень від постачальників до посередників, а потім — від посередників до споживачів. Така задача має назву двохетапної транспортної задачі.

63.Сформулюйте другу теорему двоїстості і дайте її економічне тлумачення.

Між розв’язками спряжених задач крім рівності значень цільових функцій існує тісніший взаємозв’язок. Теорема (друга теорема двоїстості для симетричних задач). Для того, щоб плани X* та Y* відповідних спряжених задач були оптимальними, необхідно і достатньо, щоб виконувалися умови доповнюючої нежорсткості:

(3.20) (3.21)

Доведення. Необхідність. Нехай X* та Y* — оптимальні плани відповідно прямої та двоїстої задач (3.20) i (3.21). З першої теореми двоїстості відомо, що а також компоненти векторів X* та Y* задовольняють системи обмежень задач (3.20) та (3.21), тобто:

, (3.24) . (3.25) Помножимо (3.24) на , а (3.25) — на і підсумуємо праві та ліві частини. Отримаємо: ; . Праві частини останніх двох нерівностей не збігаються, але оскільки їх ліві частини однакові, то це означає, що разом вони виконуються лише за умови рівностей, тобто: ; .

Виконаємо перетворення для кожного рівняння: ; (3.26) . (3.27)

Оскільки , то в рівнянні (3.26) кожна з компонент , а , тому виконання рівняння (3.26) можливе лише у тому разі, коли кожний доданок виду . Аналогічне міркування проведемо для (3.27), після чого можна висновувати, що . Отже, необхідність умов додаткової нежорсткості доведено.

Достатність. За умовою виконуються рівняння , ,

Необхідно довести, що X* та Y* — оптимальні плани відповідно прямої (3.20) та двоїстої (3.21) задач. У кожному рівнянні розкриємо дужки та підсумуємо перше рівняння по , а друге — по . Отримаємо: ; . Ліві частини цих рівнянь однакові, отже, . Тоді за першою теоремою двоїстості, оскільки значення цільових функцій цих задач збігаються, можна висновувати, що X* та Y* — оптимальні плани спряжених симетричних задач. Теорему доведено. Очевидніший взаємозв’язок між оптимальними планами прямої та двоїстої задач встановлює наслідок другої теореми двоїстості.

Наслідок. Якщо в результаті підстановки оптимального плану однієї із задач (прямої чи двоїстої) в систему обмежень цієї задачі і-те обмеження виконується як строга нерівність, то відповідна і-та компонента оптимального плану спряженої задачі дорівнює нулю.

Якщо і-та компонента оптимального плану однієї із задач додатна, то відповідне і-те обмеження спряженої задачі виконується для оптимального плану як рівняння.

Економічний зміст другої теореми двоїстості стосовно оптимального плану Х* прямої задачі. Якщо для виготовлення всієї продукції в обсязі, що визначається оптимальним планом Х*, витрати одного і-го ресурсу строго менші, ніж його загальний обсяг , то відповідна оцінка такого ресурсу (компонента оптимального плану двоїстої задачі) буде дорівнювати нулю, тобто такий ресурс за даних умов для виробництва не є «цінним».

Якщо ж витрати ресурсу дорівнюють його наявному обсягові , тобто його використано повністю, то він є «цінним» для виробництва, і його оцінка буде строго більшою від нуля.

Економічне тлумачення другої теореми двоїстості щодо оптимального плану Y* двоїстої задачі: у разі, коли деяке j-те обмеження виконується як нерівність, тобто всі витрати на виробництво одиниці j-го виду продукції перевищують її ціну сj, виробництво такого виду продукції є недоцільним, і в оптимальному плані прямої задачі обсяг такої продукції дорівнює нулю.

Якщо витрати на виробництво j-го виду продукції дорівнюють ціні одиниці продукції , то її необхідно виготовляти в обсязі, який визначає оптимальний план прямої задачі .