8. Математическое описание надежности систем, структурные функции. Системы «k из n» Общая постановка

Рассматривается система, состоящая из n элементов, каждый из которых может быть работоспособным и не работоспособным. Состояния различных элементов, если не оговорено другое, предполагаются независимыми друг от друга. Состояние всей системы описывается n-мерным бинарным вектором x=(x₁,…,x_n), i-я компонента которого характеризует состояние i-го объекта: x_i = (Работоспособен i-й элемент)?1:0. (8.1)

Структурные функции

Система в целом также может быть работоспособна, что описывается структурной функцией: ф(x)= (Система работоспособна)? 1 : 0; (8.2)

Свойства

1. ф(0,…,0)=0;

2. ф(1,…,1)=1;

3. если 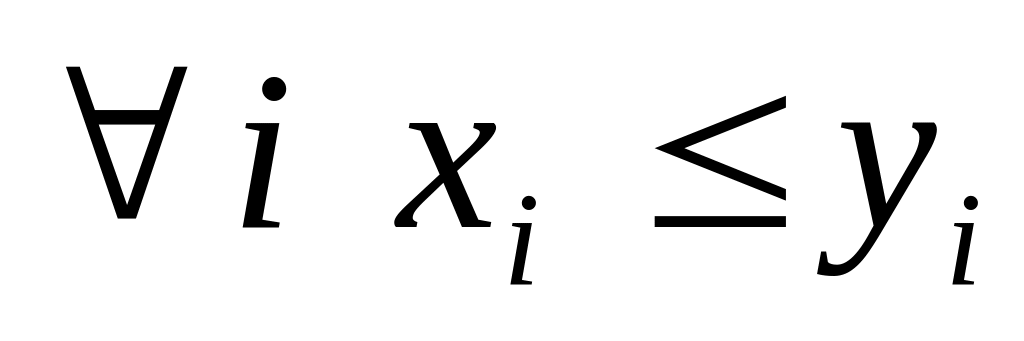, то ф(x)≤ ф(y) (монотонность)

Индикаторы состояний x_i элементов бывает удобно трактовать как булевы переменные и просто как числа 1 и 0.

Формулы преобразования логических выражений в арифметические

A^B=AB; AvB=1-(1-A)*(1-B)=A+B-AB; . (8.3)

Для всех элементов заданы вероятности их работоспособности p_i=P {x_i=1}. Для невосстанавливаемых элементов это может быть вероятность безотказной работы на заданном интервале времени P_i(t); для восстанавливаемых – нестационарный коэффициент готовности К_гi(t), или стационарный коэффициент готовности К_гi.

Требуется определить вероятность работоспособности системы P = P{ф(x)=1}.

Заметим, что эта вероятность равна математическому ожиданию ф(x):

M [ф(x)]=1*P {ф(x)=1}+0*P{ ф(x)=1}=P

Аналогично p_i = M x_i

Поэтому

, (8.4)

Где p(x) – вероятность нахождения системы в состоянии x, вычисляемая по формуле:

P(x) = (8.5)

Системы «k из n»

Определение

Система «k из n» - это система из n элементов, которая работоспособна тогда и только тогда, когда в ней работоспособны не менее k элементов.

Структурная функция

Из определения получается, что

{1, если x₁+…+x_n ≥ k;

ф(x)={

{0, если x₁+…+x_n < k.

(8.6)

Последовательная и параллельная системы являются частными случаями систем «k из n»:

«n из n» и «1 из n» соответственно.

Вероятность работоспособности системы

Если все элементы системы «k из n» равнонадежны, что часто бывает на практике, т.е. для всех элементов p_i = p, то вероятность работоспособности системы выражается формулой

(8.7)

Где - число сочетаний из n элементов по j. (8.8)

Средняя наработка системы до отказа

Если длительности безотказной работы всех элементов имеют показательное распределение с одинаковым средним T_e­, то средняя наработка системы до отказа

T=(1/k+…+1/n)T_e (8.9)

(доказательство аналогично случаю параллельной системы)

Системы «2 из 3»

На практике часто используются системы «2 из 3». Для них структурная функция имеет вид:

ф(x)=x₁x_{2 V} x₁x₃ v x₂x₃ = x₁x₂ + x₁x₃ + x₂x₃ - 2 x₁x₂x₃ (8.10)

Откуда

P=p₁p₂ + p₁p₃ + p₂p₃ - 2p₁p₂p₃ (8.11)

9. Последовательные системы, расчет их надежности

Последовательной называется система, которая работоспособна тогда и только тогда, когда работоспособны все её элементы.

Несмотря на схожесть изображения, соединение элементов в смысле надежности надо отличать от их физического (электрического) соединения. Например, параллельно соединенные конденсаторы с точки зрения теории надежности могут рассматриваться как последовательная система, так как при пробое одного конденсатора перестает работать вся схема.

Структурная функция

Структурная функция последовательной системы может быть выражена различными способами:

(во всех операциях i=1,…,n) (9.1)

Вероятность работоспособности системы

Для вероятности работоспособности системы на основании теоремы умножения вероятностей получим:

(9.2)

Этот же результат можно получить, используя свойства математического ожидания:

(9.3)

Пусть q_i=1-p_i <<1, Тогда для Q = 1 – P получим:

(9.4)

Наработка до отказа

Наработка до отказа последовательной системы с невосстанавливаемыми элементами

(9.5)

Интенсивность отказов

Пусть известны интенсивности отказов элементов λ_i(t). Обозначим через λ(t) интенсивность отказов системы. Тогда для любого t

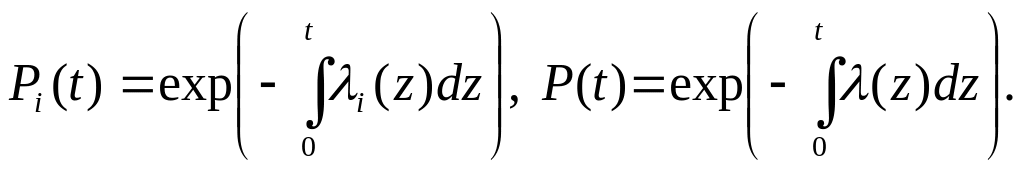
С другой стороны,

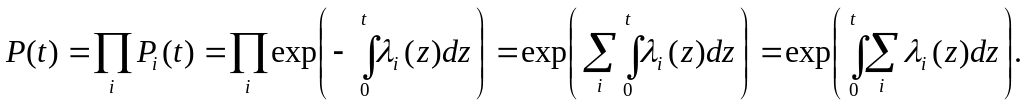
Поэтому

(9.6)

В частности, если все элемент имеют постоянные интенсивности отказов λ_i, то и система имеет постоянную интенсивность отказов, равную

(9.7)

Нередко в большой системе можно выделить группы элементов, имеющих одинаковую интенсивность отказов. В этом случае формулу (9.7) можно преобразовать. Пусть k – число групп элементов, n_j – число элементов в j-й группе (n_i+…+n_k=n), λ_j – интенсивность отказов каждого из элементов j-й группы. Тогда

(9.8)

Для расчета средней наработки до отказа в общем случае можно использовать формулу (2.2): T=

В случае показательных распределений наработки до отказа элементов со средними T_i = λ_i^‑1, из (9.7) получим:

(9.9)