Показательное распределение

Т.к. обычно стараются объект использовать только в период нормальной работы, можно считать величину λ(t) как постоянную величину λ. Подставив это в формулу (2.8) (это формула вероятности безотказной работы через интенсивность отказов), получим P(t)=e^-λt. Это и есть экспоненциальное или показательное распределение.

Математическое ожидание случайной величины, имеющей показательное распределение, T = 1/ λ.

(вспомним, что T мы обозначали среднюю наработку до отказа, равную мат. ожиданию от случ. величины)

Характеристическим свойством показательного распределения является отсутствие памяти, т.е. вероятность безотказной работы на каком-то интервале (s,s+t) НЕ ЗАВИСИТ от времени предшествующей работы s, а зависит только от ДЛИНЫ ИНТЕРВАЛА t. (Если объект сейчас работоспособен, то его будущее поведение не зависит от прошлого)

P { ξ ≥ s+t | ξ ≥ s } = (2.9)

Если время намного меньше средней наработки до отказа, t<<T, т.е. λt<<1, то можно использовать упрощенную формулу:

P(t) ≈ 1 – t/T = 1 – λt (2.10)

Погрешность этой формулы не превосходит (t/T)² / 2, причем точное значение всегда будет больше приближенного. Она вытекает из разложения экспоненты в степенной ряд.

3. Восстанавливаемый объект с мгновенным восстановлением. Распределение числа отказов за заданное время.

Восстанавливаемый объект – объект, у которого восстановление работоспособного состояния предусмотрено в «регламенте»;

Восстанавливаемый объект с мгновенным восстановлением.

(Реальное время восстановления больше 0, но если оно гораздо меньше периодов работы, то можно им и пренебречь)

Пусть ξ₁ – наработка до первого отказа, ξ₂ – наработка МЕЖДУ первым и вторым отказами. Эти величины – независимые и имеют одно и то же распределение F(t) = P { ξ_i < t }.

Распределение числа отказов

Основной характеристикой в этой модели является число отказов за время t – v(t). Для получения распределения этой случайной величины используется то, что

P { v(t) ≥ n } = P { ξ₁ + ξ₂ + … + ξ_n < t }

Если распределение является показательным, т.е. F(t) = 1 – e^-λt, v(t) имеет пуассоновское распределение P {v(t) = n } = (3.1).

Практические оценки числа отказов

В общем случае для практических оценок числа отказов на большом интервале времени можно использовать тот факт, что v(t) асимптотически нормально при t→∞ (или стремится к нормальному распределению или гауссовскому).

М ат. ожидание M v(t) → t/T;

Дисперсия D v(t) →

, где σ² = D ξ_i , а T = M ξ_i

Этот факт, что v(t) стремится к гауссовскому, показывает предел:

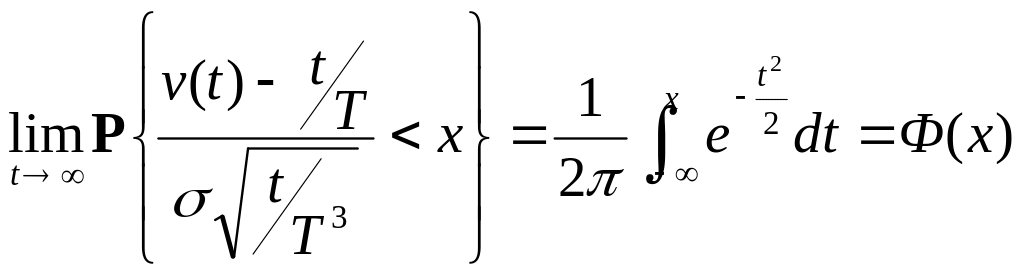(3.2)

Использование квантилей нормального распределения.

Пусть некоторый элемент имеет среднее время наработки до отказа T=100 ч, среднеквадратичное отклонение σ = 60 ч и требуется с достоверностью 0,95 оценить число запасных элементов, необходимое для работы в течение времени t = 8000 ч.

Р ешение. По таблице квантилей нормального распределения найдем квантиль уровня 0,95, т.е. такое число u_0,95, чтобы Ф(u_0,95) = 0,95. Получим u_0,95 = 1,65. Тогда с вероятностью 0,95 выполняется неравенство

,

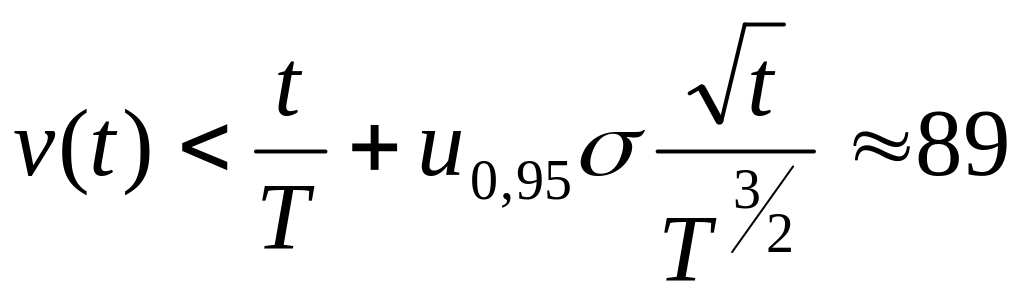Т.е. нужно иметь 89 элементов.