2. Невосстанавливаемый элемент. Вероятностные и статистические определения основных характеристик надежности.

Невосстанавливаемый объект - объект, у которого восстановление работоспособного состояния предусмотрено в «регламенте».

Вероятность безотказной работы и показатели, связанные с наработкой. Вероятность безотказной работы

Обозначим через ξ (кси) время работы (наработку) объекта до отказа. Это – случайная величина, и её можно охарактеризовать функцией распределения F(t) – функцией, показывающей вероятность того, что значение случайной величины меньше её аргумента t: F(t) = P { ξ < t }. (t – время, и оно больше или равно 0). Будем считать, что существует f(t)=F’(t) – плотность распределения.

Функция P(t) = 1 – F(t)= P { ξ >= t } – называется вероятностью безотказной работы за время t.

Статистическая оценка вероятности безотказной работы

P^(t) = N(t) / N (2.1)

N(t) – число объектов, безотказно проработавших время t, а N = N(0) – первоначальное количество исправных объектов.

Средняя наработка до отказа

T = M ξ = (к последней форме записи мы перешли с помощью формулы интегрирования по частям)

Полученная формула:

T= (2.2)

Статистическая оценка средней наработки до отказа

(2.3), где t_i – наработка до отказа i-го элемента.

Гамма-процентная наработка до отказа

Наработка, в течение которой отказ объекта не возникнет с вероятностью γ, выраженной в процентах. Она обозначается T_γ и является корнем уравнения

F(T_γ) = 1 – γ/100 или P(T_γ) = γ/100 (2.4)

(F(t) – функция распределения от кси – наработки до отказа, P(t) – вероятность того, что откажет в момент времени t; подробно – см. выше)

Обычно для гаммы задают значения 90; 95; 99; 99,5% и другие. Тогда вероятность до отказа будет 0,1; 0,05; 0,01 и 0,005 и др.

Статистическая оценка наработки до отказа

Для статистической оценки T_γ необходимо упорядочить по возрастанию полученные в результате испытаний значения наработок до отказа t_i. Получится вариационный ряд. И из этого ряда надо выбрать значение с номером [(1-γ/100)N]. Это и будет статистической оценкой наработки до отказа:

(2.5)

Примечание: Господин Нетес В.А. на лекции говорил, что в методичке опечатка, и поэтому тут приведена формула, которую он давал на занятии.

Интенсивность отказов

Важной характеристикой, наглядно показывающей, как меняется надежность объекта со временем, является интенсивность отказов λ(t) – величина, показывающая вероятность того, что объект, проработавший безотказно, откажет в следующую единицу времени.

Размерность интенсивности отказов λ(t) – [единица наработки]^-1

Получаем, что для расчета λ(t) надо взять вероятность отказа на интервале от t до t+Δt с условием, что до момента t отказ не возник, разделить эту вероятность на длину интервала (Δt), и устремить Δt к нулю.

Шайтан-Матан:

P { t < ξ < t + Δt | ξ ≥ t } = P { t < ξ < t + Δt } / P { ξ ≥ t } =

(разделим на ,перейдем к пределу при →0 и получим:)

(2.6)

Статистическая оценка интенсивности отказов

(2.7)

Выражение вероятности безотказной работы через интенсивность отказов

Решая (2.6) как дифференциальное уравнение относительно P(t), получим:

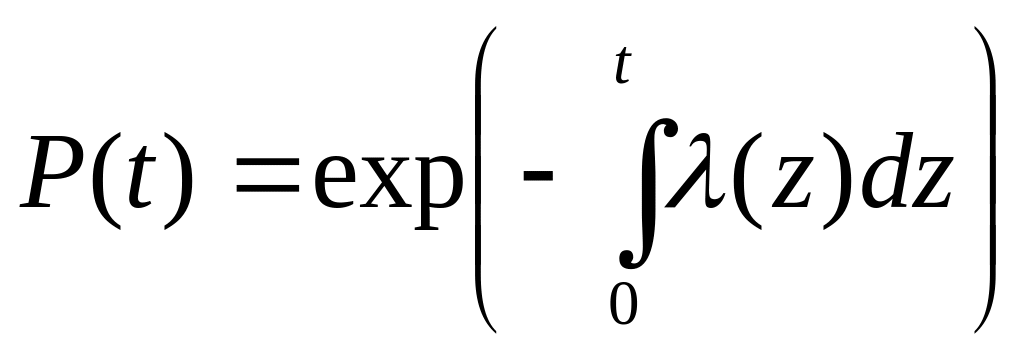. (2.8)

Любая из функций F(t), f(t), P(t) и λ(t) полностью определяет распределение наработки до отказа, и остальные три функции могут быть выражены через неё.

График типичной зависимости λ(t) и периоды времени отказов.

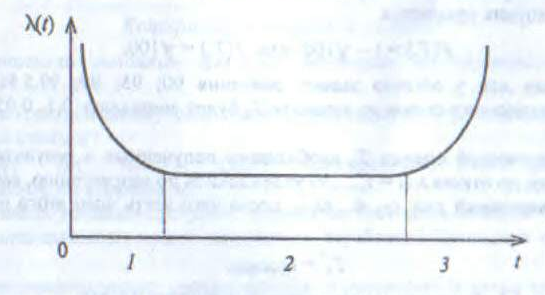
На графике видно, что есть три интервала времени (периода):

1. Интервал приработки;

2. Интервал нормальной работы;

3. Интервал старения.

Период приработки обладает повышенной интенсивностью отказов. Это связано с тем, что объекты могут иметь скрытые дефекты, влекущие отказы вскоре после начала работы. Так же возможно, что обслуживающий персонал может еще не вполне освоить новый объект, что чаще приводит к более частым отказам. По мере устранения указанных причин λ(t) убывает.

Период нормальной работы характеризуется постоянным (или почти постоянным) значением λ(t). Чаще всего стараются сделать так, чтобы объект использовался по назначению именно в этот период работы.

В период старения необратимые явления (механические, физические, химические) приводят к ухудшению объекта, из-за чего λ(t) возрастает. Часто наступление периода старения рассматривается как критерий предельного состояния.