19. Системы с аддитивным выходным эффектом (общее понятие и важнейшие частные случаи), расчет их коэффициента сохранения эффективности Система с аддитивным выходным эффектом

Пусть система состоит из нескольких подсистем G₁,...,G_k (вообще говоря, пересекающихся), выходной эффект всей системы представляет собой сумму значений выходного эффекта подсистем (особенность системы именно такого вида), а каждая подсистема является изделием вида I. Обозначим через w_j «вес» j-й подсистемы, т.е. долю, вносимую ей в общую номинальную эффективность Ео: W_J=E_0j/E₀, где Eoj - номинальная эффективность j-й подсистемы

(E₀=∑jE_0j). Тогда, обозначая через ф_i(х) структурную функцию j-й подсистемы, получим:

(19.1)

откуда

. (19.2)(1)

Где p_j – вероятность работоспособности j-й подсистемы.

Возможные случаи Иерархическая ветвящаяся структура

Рассмотрим два частных случая систем с аддитивным выходным эффектом. Типичной для многих технических систем, к числу которых относятся многие управляющие, информационные, вычислительные и другие системы, является иерархическая ветвящаяся структура. В таких системах элементы самого нижнего уровня называют обычно исполнительными. Пусть каждый нормально функционирующий исполнительный элемент вносит свой вклад в общий выходной эффект системы. При этом такой элемент считается нормально функционирующим, если работоспособен как он сам, так и вся цепочка элементов верхних уровней, которым он подчинен. В этом случае можно применить формулу (19.2), в которой G_j - подсистема, состоящая из j-го исполнительного элемента и всех вышестоящих элементов, которым он подчинен ; w_j – вклад j-ro исполнительного элемента.

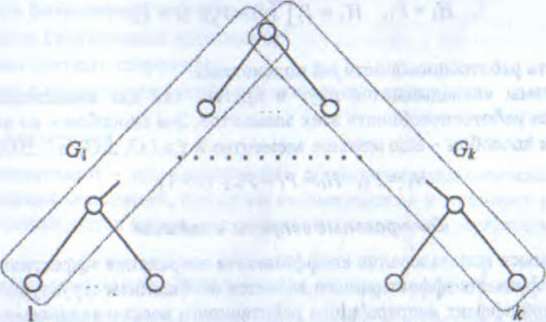
Система с иерархической ветвящейся структурой.

Сеть связи

Рассмотрим теперь сеть связи. В качестве ее подсистем выделим подмножества элементов, обеспечивающих связь между различными парами корреспондирующих узлов. Обозначим через P_ij вероятность возможности связи между узлами i и j (для упрощения предполагается, что связь или существует, или нет), а через w_ij - долю трафика между парой узлов i и j в общей величине трафика в сети. Тогда

(19.3)

В зависимости от ситуации трафик может оцениваться по-разному: временем занятия, числом типовых каналов, объемом передаваемой информации и т.п.

20. Мультимодальные системы, расчет их коэффициента сохранения эффективности

Мультимодальной называется система, которая может функционировать (решать стоящую черед ней задачу) несколькими способами, причем каждый раз выбирается тот из возможных в данном состоянии способов, который даст максимальный эффект. Пусть имеется т способов функционирования и V_l - значение выходного эффекта при l-м способе. Считаем, что способы упорядочены по убыванию их эффективности:

v₁ ≥ v₂ ≥ … ≥ v_m. Тогда

, (20.1)

Где H_l - вероятность реализации 1-го способа.

Обозначим через G_l подсистему, обеспечивающую l-й способ функционирования. Для простоты так же обозначим и событие, состоящее в ее работоспособности, а событие ее неработоспособности - G_l’. Система решает задачу l-м способом, если подсистема G_l работоспособна, а все подсистемы с меньшими номерами - нет.

Поэтому H_l = P(G1’...G_l-1'G_l). Для расчета этих вероятностей надо сначала выразить события G_k' и G_l через индикаторы работоспособности элементов х_l, затем аналогично тому, как это описано применительно к формуле (16.1), привести соответствующие логические выражения к бесповторной форме, используя правила поглощения (16.2)-(16.4), и, наконец, подставить в них вероятности работоспособности элементов.

В двух частных случаях можно записать простые явные формулы для вычисления вероятностей H_j.

1. Каждый элемент может входить в состав только одной подсистемы, т.е. подсистемы попарно не пересекаются. В этом случае

(20.2)

,где Рj - вероятность работоспособности j-й подсистемы.

2. Подсистемы «вкладываются друг в друга», т.е. для выполнения задачи 1-м способом требуется работоспособность всех элементов, 2-м способом - не все элементы, а лишь их часть, 3-м способом - еще меньше элементов и т.д.: G₁ﬤG₂ﬤ…ﬤG_m. Тогда

(20.3)